Hipotez Testleri: Grup Karşılaştırmaları, A/B Testi

Bir web sitesinde yapılan arayüz değişikliğinin ardından, kullanıcıların web sitesi üzerinde geçirdikleri günlük ortalama sürede bir değişiklik olduğunu düşünelim. Bu durumun şans eseri olup olmadığını gözlemlemek adına, arayüz değişikliği öncesi gözlemlenen kullanıcı grubu (A) ve değişiklik sonrasında gözlemlenen kullanıcı grubu (B) incelenmelidir. A ve B gruplarının arayüz değişikliğine bağlı olarak sitede geçirdikleri sürede herhangi bir anlamlı fark olmadığı yönünde bir hipotez kurulur ve bu hipotez test edilir.

Hipotez: Bir inanışı veya savı test etmek için kullanılan istatistiksel bir olgudur.

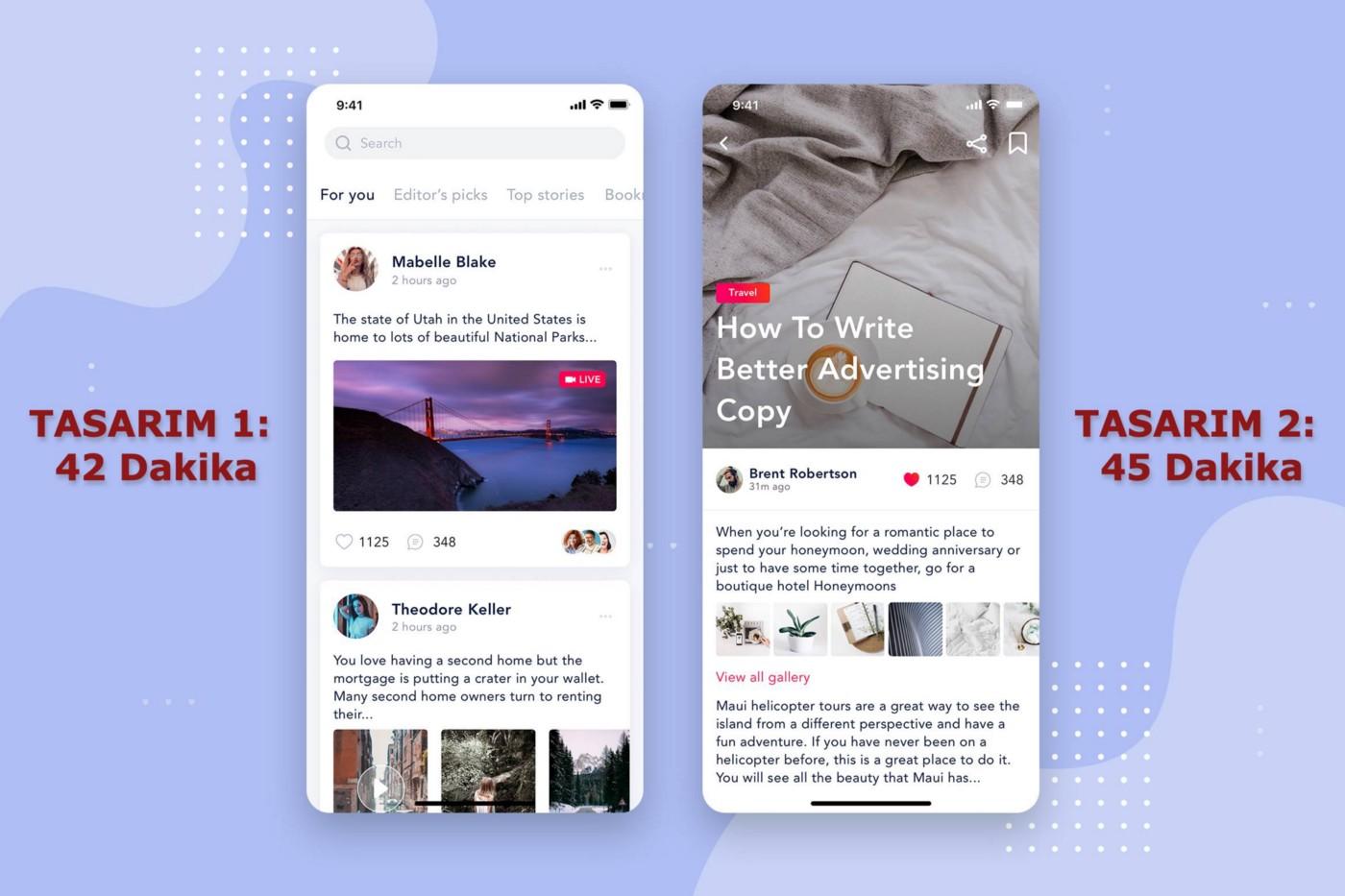
Yukarıdaki görselde bir internet sitesi için hazırlanan iki farklı tasarım görülmektedir. Her iki tasarımın da bir grup kullanıcı tarafından test edildiğini ve test gruplarının sitede geçirdikleri ortalama sürelerin 42 ve 45 dakika olduğunu düşünelim. İlk bakışta 3 dakikalık farkın kullanıcı deneyimi açısından daha verimli olduğu düşünülse de elde edilen farkın şans eseri oluşmuş olma ihtimali göz önünde bulundurulmalıdır. Bir örneklem üzerinden bir genelleme yapmaya çalıştığımız bu senaryoda, elde edilen 3 dakikalık farkın şans eseri ortaya çıkmadığı, tasarım değişikliğinin kullanıcıların sitede geçirdikleri süre üzerinde etkili bir değişken olduğu istatistiki bir yöntem ile ispat edilmesi gerekmektedir.  

A/B testi

İki grup ortalaması arasında karşılaştırma yapılmak istendiğinde kullanılır. Buradaki A ve B harfleri ‘Kontrol Grubu’ ve ‘Deney Grubu’nu ifade eder. Genellikle deneme yapılması istenilen özelliklerin testi için bir takım makine öğrenmesi algoritmaları sayesinde, farklılıkların test edilmesi gibi senaryolarda kullanılır. A/B Testleriyle karşılaşıldığında genellikle iki ortalama değer veya iki oranın kıyaslandığı düşünülür.

Bağımsız iki örneklem T testi

‘Bağımsız İki Örneklem T Testi’ iki grup ortalaması arasında karşılaştırma yapılmak istendiğinde kullanılır.

H₀ yokluk hipotezi olup, sınamak istediğimiz durum bu hipotezdir. Analizlerde H₀ hipotezi test edilir. H₀ hipotezini reddetme veya reddedememe durumuna göre, H₁ hipotezi değerlendirilir. Hipotezler görseldeki gibi 3 farklı şekilde kurulabilir. 

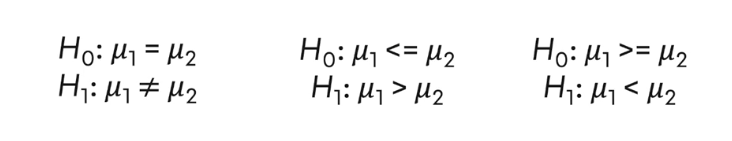
İki grubun ortalaması kıyaslanırken kullanılan bazı test istatistikleri mevcuttur:

Burada X1 ve X2 örnek ortalamaları farkı istatistiği, S örnek varyansı istatistiği iken t test istatistiğini belirtir. Bu bağlamda, bilimsel kıyaslamalar ve karara varma imkanı sağlayan yöntemlerin bazı varsayımları vardır:

Normallik

Grupların standart normal dağılıma sahip olması varsayımıdır yani ortalamanın 0, standart sapmanın 1 olması demektir.

Varyans Homojenliği

İki grubun varyanslarının homojen olması varsayımıdır yani iki grubun dağılımlarının birbirine benzer olması durumudur.

Hipotez testlerinin işleyişinde, test istatistiklerinin yanı sıra hipotezler p-value değerlerinin kullanılması ile de yorumlanabilir. Bu doğrultuda işleyiş akışı aşağıdaki gibi olacaktır:

(P-Value, gözlemlenen sonuçların, test edilmek istenen durumla alakalı olmamasının olasılığıdır.)

1. Hipotezler (H₀ ve H₁) kurulur.
2. İlgili hipotezin gerekli varsayımları olması dahilinde, varsayımlar incelenir. İncelenen varsayımların durumuna göre parametrik ya da non-parametrik yöntemler kullanılır. Gerekli görülmesi halinde veri ön işleme ve keşifçi veri analizi teknikleri de uygulanır. Bu kapsamda da varsayımlar için hipotez testleri kurulur ve burada kurulan H₀ testinin reddedilememesi tercih edilir.
3. ‘Parametrik’ veya ‘Non-Parametrik’ yöntemlerin sonucunda elde edilen p-value ile hipotezler yorumlanır. Dağılımlar incelendiğinde aykırı gözlemlerin mevcut olduğu çarpık dağılımlarda istatistiksel betimleme olarak medyan tercih edilirken simetrik dağılımlarda ortalama kullanılır. Parametrik testlerde simetrik dağılımlar çerçevesinde ortalamalar kullanılırken, non-parametrik testlerde medyanlar kullanılır.

İki örneklem oran testi (İki grup oran karşılaştırma)

Önceki bölümde uygulanan testlerde grup ortalamaları ve medyanlar kıyaslanmıştı. Şimdi iki oran arasındaki karşılaştırmalara bakalım:

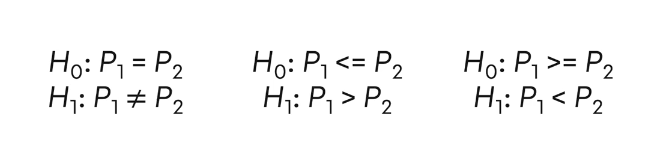
İki Örneklem Oran Testi Hipotezleri

Yukarıda hipotez testlerini kurma noktasında kullanılan hipotez çeşitleri gösterilmektedir. Bu bağlamda Zh olarak isimlendirilen istatistiksel bir değer mevcuttur. Aşağıdaki görselde Zh değerinin hesaplanmasında kullanılan formül verilmiştir.

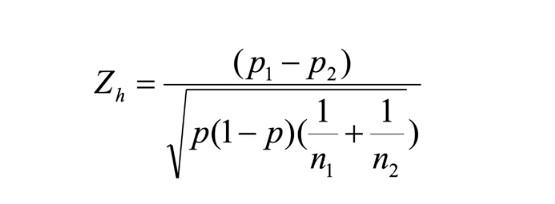
Zh istatistiği iki oranın farkları ve iki oran için örneklem sayılarına dayalı bir hesaplamayı barındırmaktadır. Lakin Zh ile hesap yapmak yerine daha kolay bir yol olan p-value değerini kullanarak, daha pratik bir şekilde kararlar verilebilir. Bu değer neticesinde bir H₀ hipotezinin reddedilip reddedilmeyeceğine karar verilir. Burada kullanılan varsayım iki grup için de örneklem sayılarının 30’dan büyük olmasıdır.

Bu bağlamda amaç, iki orandan oluşan grupların arasındaki farklılıkların var olup olmadığını ve bu farklılıkların şans eseri oluşup oluşmadığını istatistiki bir şekilde ifade edebilmektir.

İkiden Fazla Grup Ortalamasının Karşılaştırılması (ANOVA-Analysis of Variance)

Şimdi A/B testleri kapsamında gruplar arasında farklılık olup olmadığını ANOVA özelinde gözlemleyelim. Hipotezlerin kurulumu grupların ortalamaları özelinde olacaktır:

ANOVA hipotezleri

Grup ortalamalarını kıyaslarken hipotezler, ortalamalar birbirine eşittir veya değildir şeklinde kurulur. Bu kapsamda yine p-value incelenebilir. Birçok istatistik yazılımında p-value, ‘Sig.‘ veya ‘Significance’ olarak görülebilir. p-value, ‘anlamlılık değeridir.

ANOVA işleyiş akışını betimlersek, önceki tekniklere benzer şekilde:

1. Hipotezler Kurulur.
   H₀: (M₁=M₂=M₃=M₄) Grup ortalamaları arasında fark yoktur.
   H₁: Grup ortalamaları arasında fark var.
2. Varsayım Kontrolleri yapılır: Normallik varsayımı, varyans homojenliği varsayımı
   (Bu kapsamda varsayım sağlanıyorsa ‘tek yönlü Anova (one way anova)’, varsayım sağlanmıyorsa ‘kruskal’ metotları - Bu metot normal dağılım göstermeyen gruplarda üç veya daha fazla sayıda grubun ortalamaları arasındaki farklılığın anlamlılığını test amacıyla kullanılan bir tekniktir. -  kullanılır.)
3. Hipotez testi ve p-value değeri incelenerek hipotez yorumlanır.

Grup karşılaştırmaları, A/B testleri ve ölçümleme problemleri hakkında detaylı bilgi edinmek isterseniz Miuul'un Ölçümleme problemleri üzerine oluşturduğu eğitimleri inceleyebilirsiniz. Veri bilimini kariyer yolunuz haline getirmek istiyorsanız, Miuul’un Veri Bilimci Kariyer Yolculuğu tam olarak aradığınız eğitimi sizlere sunacaktır.

Kaynaklar

• Veri Bilimi Okulu, AB Testi Nedir ? İstatistiksel A/B Testleri Nasıl Yapılır?
• Statistics How To,  Hypothesis Testing
• Towards Data Science, Everything You Need To Know about Hypothesis Testing — Part I
• Miuul, Ölçümleme Problemleri