Veri Biliminde Zaman Serileri
Zaman serileri
Geçmişten gelen gözlemlerin mevsimsellik, trend ve durağanlık özelliklerini kullanarak gelecek için stratejik bir tahminde bulunmayı sağlayan bir alandır. Bu alan birçok çeşitli sektörde farklı amaçlar için kullanmaktadır. Bu yazımızda zaman serilerini detaylarıyla inceleyeceğiz.
Zaman serisi, zamana göre sıralanmış gözlem değerlerinden oluşan veridir. Zaman serisi verileri, farklı veya düzenli zaman aralıklarında kaydedilen bir dizi veri noktası veya gözlemdir. Kaydedilen veri noktalarının sıklığı saatlik, günlük, haftalık, aylık, üç aylık veya yıllık gibi belirli periyotlarda olabilir. Örnek olarak hava durumu, borsadaki bir hisse senedi değeri verilebilir. Zaman serilerinde birçok yöntem kullanılmakla birlikte temel amaç tahmin başarısı en iyi olan istatistiksel modeli tercih etmektir.
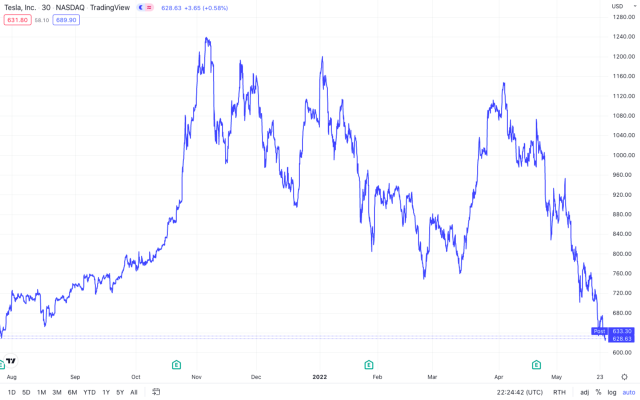
Zaman serileri üzerinde çalışmayı hedefleyen bir veri bilimci, zaman serilerinin doğasını iyi kavramalıdır. Öyle ki, bir zaman serisi ile karşılaştığında, bu seri üzerinde yaptığı gözlemler sonucunda, serinin yapısı ve yönelimi hakkında yorum yapabilmelidir. Veri bilimciler zaman serileri kapsamında bir takım tahminler gerçekleştirmek ister. Bu tahminler, geçmiş sonuçlara dayalı olarak bir zaman serisinin gelecekteki değerlerini tahmin etmek için istatistiksel bir model kullanma sürecidir. Zaman serisi analizini kullanan tahmin verileri, bilinen geçmiş sonuçlara dayanarak gelecekteki sonuçları tahmin etmek için bazı önemli modellerin kullanımını içerir.
Zaman serilerini anlamlandırma aşamasında kullanılan birkaç kavram mevcuttur:
- Durağanlık (Stationary)
- Trend
- Mevsimsellik (Seasonality)
- Döngüsellik (Cycle)
Bu kavramları tespit etme aşamasında kullanılan çeşitli istatistiki testlerin olmasının yanı sıra, veri bilimciler bazı durumlarda sadece görsel inceleme ile de bu kavramlar hakkında yorum yapabilir..
Durağanlık (stationary)
Durağanlık, bir serinin istatistiksel özelliklerinin zaman içerisinde değişime uğramamasıdır. Durağanlığı incelemek için bir takım istatistiki testler kullanmak gerekmektedir.
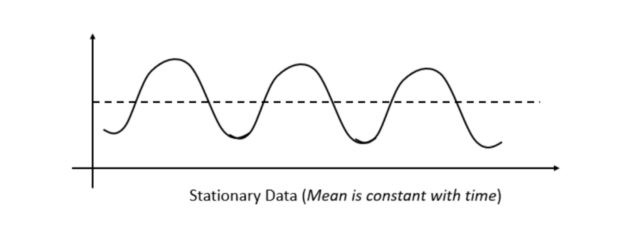
Bir zaman serisinin ortalaması, varyansı ve kovaryansı zaman boyunca sabit kalıyorsa, (veya istatistiki olarak çok ufak farklılıklara sahipse) serinin durağan olduğu ifade edilir.
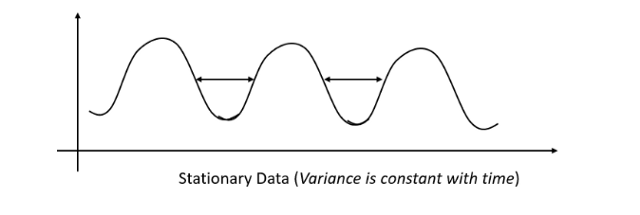
Zaman serisi verilerinin yapısı belirli bir örüntüde olduğu durumlarda, kolay tahmin edilebilir olarak nitelendirilir. Bu kapsamda zaman serisinin istatistiki özellikleri değişmediği durumlarda, başka bir deyişle serinin durağan olduğu durumlarda, çeşitli zaman periyotlarındaki değerler daha kolay tahmin edilebilir. Bir seride durağan olmama durumunun gözlemlenmesi halinde, genellikle serinin belirli zaman periyotlarında farkı alınır ve seri durağan hale getirilir.
Trend
Trend bir zaman serisinin uzun vadedeki artış ya da azalışının gözlemlendiği yapıdır. Yatırım, ekonomi, iktisat ve birçok alanda, önemli çıktılar elde edilebilmesini sağlayan trend kavramı, zaman serileri başlığı altında bilgi sahibi olunması gereken en önemli konulardan biridir.
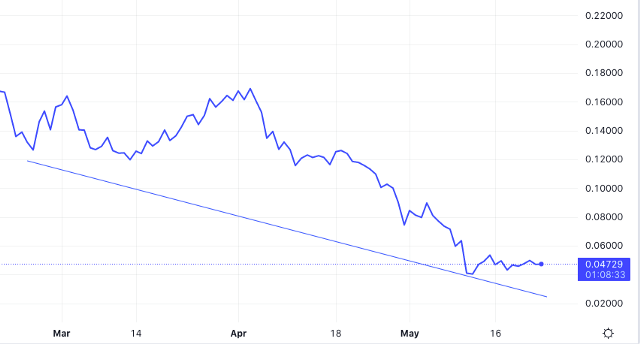
Örnek olarak yukarıda verilen görselde aylara göre azalan bir trend görülmektedir. Genel olarak, bir trend gözlenen zaman serilerinde durağanlık olmadığı söylenebilir. Bunun temel sebeplerinden biri gözlem değerlerinin trend yönünde ortalamaların artması veya azalmasıdır. Durağanlık tanımı gereği bir serinin istatistiki değerlerinin zamana göre değişmemesi gerektiğinden genel olarak trend varlığı yapısı gereği durağanlıkla uyuşmayacaktır.
Mevsimsellik (seasonality)
Zaman serisinin belirli bir davranışı belirli periyotlarla tekrar etmesi durumuna mevsimsellik denir.
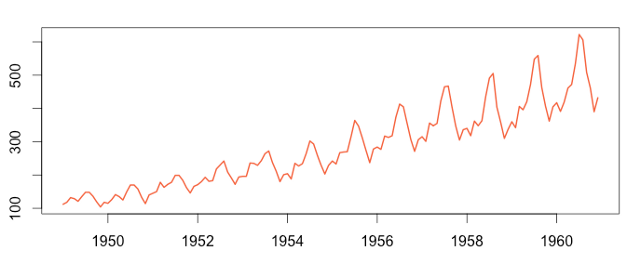
Yukarıda verilen görselde, durağan olmayan, yukarı yönlü trende sahip, mevsimsellik içeren bir zaman serisi örnek verilmiştir.
Döngüsellik (cycle)
Döngüsellik, mevsimselliğe benzer bir şekilde, tekrar eden düzenler barındırır. Farklı olarak mevsimsellik daha belirgin, kısa vadeli ve düzenli aralıklarla (gün, hafta, mevsim, yıl gibi zamanlarla örtüşecek şekilde) gerçekleşir. Döngüsellik ise daha uzun vadeli ve belirsiz yapılarda, gün/hafta/yıl gibi zaman aralıklarıyla örtüşmeyecek şekilde, daha çok yapısal nedenler ve konjonktürel değişimlerle (örneğin politikacıların ve iş dünyasındaki belirli kişilerin demeçleri ile) şekillenerek gerçekleşir.
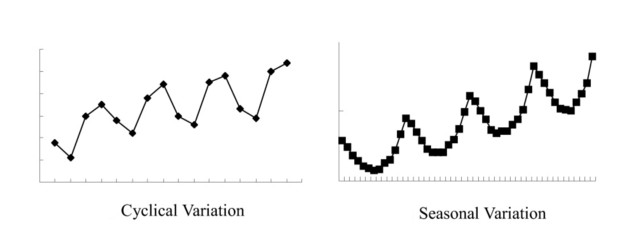
Zaman serilerinde “bir zaman periyodundaki değer, en çok kendisinden bir önceki zaman periyoduna ait değerden etkilenir” varsayımı yer alır. Bu varsayımdan yola çıkarak bir zaman serisinde tahmin edilmek istenilen değerlere ilişkin zaman serisinin mevsimsellik, döngüsellik ve durağanlık yapıları gözlemlenerek, önceki periyotlara ait ortalamalar belirli ağırlıklandırmalarla incelenerek sonuca varılabilir.
Hareketli ortalamalar
Hareketli ortalamalar yöntemi uzun süreli değerlere sahip zaman serilerinde uygulanmaktadır. Hareketli ortalamalar yönteminde serinin grafiği çizildiğinde seride inişler ve çıkışlar başka bir deyişle dalgalanmalar görülmektedir. Bu durumu ortadan kaldırmak ve belirli bir trend yakalamak için zaman serisindeki değerleri belirli bir büyüklükte kümeler halinde toplayarak aritmetik ortalama hesaplanması gerekir. Böylece serinin asıl terimleri yerine bu değerleri temsil eden ortalama değerleri kullanılır.
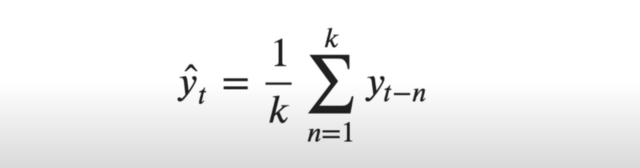
Bir zaman serisinin gelecek değeri kendisinin k adet önceki değerinin ortalaması ile temsil edilebilir. Serinin içerisinde bir t zamanındaki değer tahmin edilmek istendiğinde, ilgili zaman periyodunda belirli adet önceki değerin ortalaması alınır. Bu metoda hareketli ortalama yöntemi denir.
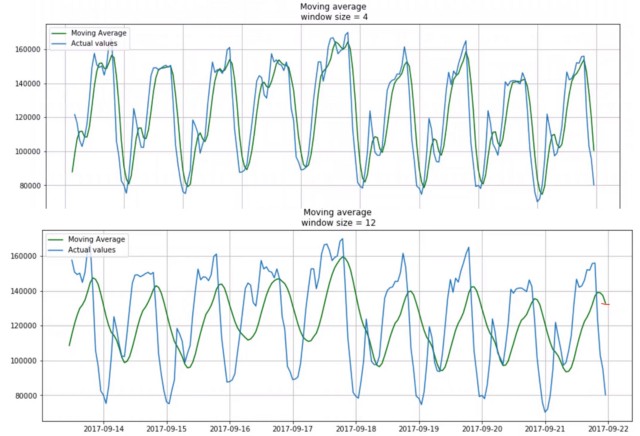
Hareketli ortalama tekniği genellikle tahmin etme yöntemi yerine bir trendi yakalamak veya gözlemlemek için kullanılır. Veri bilimi özellikle makine öğrenmesi ve istatistiksel yöntemler kapsamında özellikler türetilirken hareketli ortalamaya dayalı özellik türetimi yapılır.
Hareketli ortalamalarda zaman periyodu genişledikçe, değerlerin gidişatı daha doğru yorumlanabilir hale gelir.
Ağırlıklı ortalamalar
Ağırlıklı ortalamalar genel olarak hareketli ortalamalara benzer şekilde hesaplanmakla birlikte tahmin edilecek değere yakın zaman periyodundaki gözlemlere ağırlık vererek hesaplama fikrini taşır.
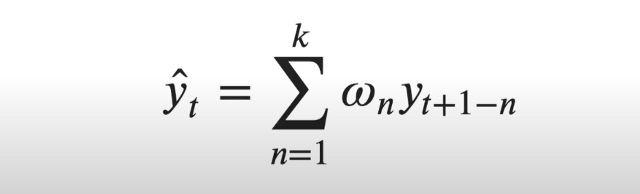
Hareketli ortalamalar önceki değerler üzerinden hesaplanacağından, temsili olacağı gelecek değerden seri yapısı kapsamında geriden gelir. Zaman serilerinde, ‘Bir zaman serisindeki gözlemler kendisinden bir önce gelen değerden en çok etkilenir’ varsayımı mevcuttur. Bu kapsamda zaman periyodunda geriye doğru gidilerek, daha önceki noktalardan tahmin edilmek istenilen nokta ile ilgili sonuçlar çıkarılmak amaçlanır. Bu durumda varsayım gereğince tahmin edilen değer, gerçek değerle oldukça farklı olacaktır. Bu sebeple temsil edilecek değere daha yakın olan önceki değerlere ağırlık verilerek hesaplama yapıldığı takdirde daha tutarlı tahmin sonuçları elde edilebilir.
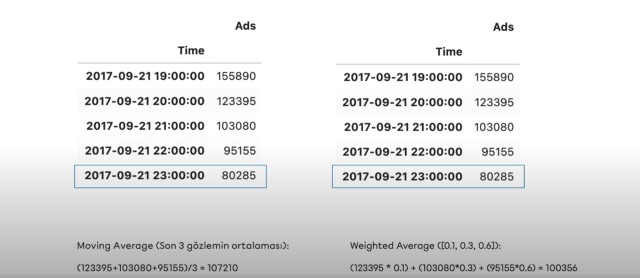
Yukarıda verilen görselde görülebildiği üzere ağırlıklı ortalamalar ile hareketli ortalamalar arasında yaklaşık olarak 7000 değerinde fark mevcut olmakla birlikte ağırlıklı ortalamalar gerçek değere daha yakın bir sonuç vermektedir.
Farklı bir bakış açısı olarak, zaman serisinde bir trend söz konusu olduğu durumlarda seriye ait değerlerin kendi ağırlıklı ortalamalarının alınmasının yanı sıra, değerlerin arasındaki artış ve azalış yüzdelerinin hareketli ve ağırlıklı ortalamaları alınarak tahminlerde bulunulabilir.
Zaman serilerinde smoothing (yumuşatma, düzeltme) yöntemleri
Smoothing, zaman serilerinde verilerin gürültü veya kesikliklerden arındırılmasını ve daha net ve kararlı bir trendin ortaya çıkmasını amaçlayan bir analitik yöntemdir. Kelime karşılığı olarak yumuşatma, düzeltme anlamı taşıyan smoothing kullanılarak zaman serilerinde çeşitli düzeltmeler yapılabilmektedir:
- Single exponential smoothing (tekil üstel düzeltme): Trend ve mevsimselliğin gözlemlenmediği durumlarda, yani yalnızca durağan serilerde kullanılır. Literatürde SES kısaltmasıyla ile de isimlendirildiği görülür.
- Double exponential smoothing (çift üstel düzeltme): SES yöntemine ek olarak serinin trendini de modelleyebilir. Ancak SES ile benzer olarak mevsimselliği yakalayamamaktadır.
- Triple exponential smoothing (üçlü üstel düzeltme): Başka bir ismi ile Holt-Winters yöntemi serinin barındırdığı trendi ve mevsimselliği yakalar. TES yöntemi, verilen üç smoothing yöntemi arasındaki en gelişmiş yöntemdir.
Şimdi bu yöntemleri detaylı bir şekilde inceleyelim:
Single exponential smoothing (SES)
SES yöntemi ağırlıklı ortalamanın genelleştirilmiş halini barındırır. Ağırlıklı ve hareketli ortalamalar ile geçmiş değerlere odaklanarak ortalama hesaplanması üzerinden düzeltme işlemi (smoothing) yapar. Bu düzeltme işlemlerinin tahmin başarısı açısından kullanılabilir olduğu varsayımı sonucunda, bu yöntemlerin farklı faktörlerle beslenmek suretiyle genelleştirilmesi ihtiyacı ortaya çıkmıştır. Bu genelleştirme ihtiyacını gidermek adına Single Exponential Smoothing yöntemi kullanıma alınmıştır. Zaman periyodunun artmasıyla birlikte SES yönteminin formülasyonunda üstellik durumu söz konusu olacaktır.
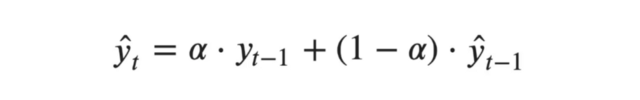
SES yönteminde:
- Üssel düzeltme yaparak tahminde bulunulur.
- Gelecek değerler, yakın geçmişte gerçekleşmiş değerlerle daha fazla ilişkilidir varsayımıyla geçmişin etkileri ağırlıklandırılır.
- Geçmiş gerçek değerler ve geçmiş tahmin edilen değerlerin üstel olarak ağırlıklandırılması ile tahmin yapılır.
- Trend ve mevsimsellik içermeyen tek değişkenli zaman serileri için uygundur.
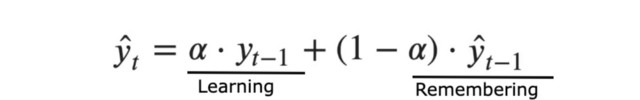
Yukarı verilen SES formülünde learning olarak verilen kısım geçmiş gerçek değeri, remembering olarak isimlendirilen kısım ise geçmiş tahmin edilen değeri temsil eder. Bu kapsamda remembering tarafında geçmişte yapılan tahmin sonuçları da (yani geçmiş modelleme kabiliyeti de) tahmin modeline alfa değeri ile belirli bir ağırlık kullanarak dahil edilirken, learning kısmında geçmiş gerçek değer başka bir deyişle öğrenilen değer olarak alfa üzerinden belirlenen bir ağırlık ile modele dahil edilir. Bu kapsamda alfa dış parametresinin yani ağırlığın alacağı değer sonucunda geçmişten gelen gerçek değer ve tahmin edilen değer arasında ağırlıklandırma ortaya konacaktır.
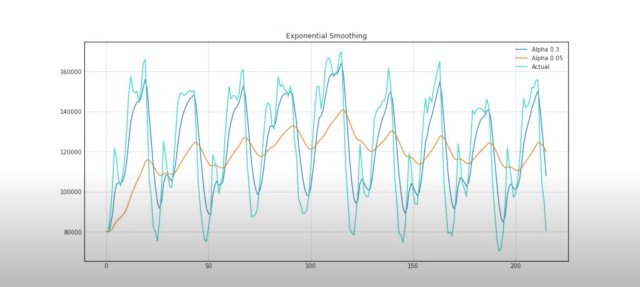
Yukarıdaki görselde yer alan örnek zaman serisinde alfanın 0.3 ve 0.05 olduğu ağırlıklar sonucunda ortaya çıkan tahmin değerleri ile gerçek değerler verilmiştir.
- Bu kapsamda alfanın 0.3 olduğu durumda SES formülü üzerinde learning kısmına yani geçmiş gerçek değere 0.3, dolayısıyla tahmin edilen remembering kısmındaki geçmiş tahmin değerine 0.7 ağırlık verilmiştir.
- Alfanın 0.05 olduğu durumda ise learning kısmı 0.05 ağırlıkta iken remembering kısmı 0.95 ağırlıkla öğrenmeye göre çok baskın bir yapıda kalmakla geçmiş tahminlere bir yapı kurulmuştur.
Sonuç olarak alfanın yüksek olduğu durumlarda öğrenme becerisine ağırlık verilirken, düşük olduğu durumlarda tahmin etme kabiliyetine ağırlık verilmiş olunur.
Double exponential smoothing (DES)
Double Exponential Smoothing yöntemi SES yöntemine ek olarak trendi de modelleyebilirdir.
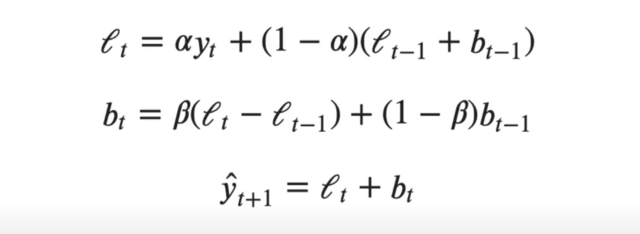
Double Exponential Smoothing yöntemi:
- Trent etkisini göz önünde bulundurarak üssel düzeltme yapar.
- DES = Level(SES) + Trend olarak betimlenir.
- Temel yaklaşım SES ile aynı olmakla birlikte trendi de içerir.
- Trend içeren ve mevsimsellik içermeyen tek değişkenli zaman serileri için uygundur.
Özetle, bir zaman aralığının tahmini değeri için bir önceki zaman aralığının level ve trend bilgisi kullanılır. Bu kapsamda level ve trend bilgileri bulunurken, alfa ve beta olmak üzere level smoothing ve trend smoothing faktörleri işlemlere dahil edilerek level ve trend için düzeltmeler yapılır. Bu kapsamda modeller kurulurken, serilerin toplamsal veya çarpımsal olması durumu gözlemlenebilir.
Toplamsal Seri
y(t) = Level +Trend + Seasonality + Noise
Bir serinin toplamsal olması durumunda mevsimsellik ve artık bileşenler, trendden bağımsızdır.
Çarpımsal Seri
y(t) = Level * Trend * Seasonality * Noise
Seride mevsimsellik ve artık bileşenler eğer trende bağımlı olarak gözlemleniyorsa, yani trende göre şekillendiği gözlemleniyorsa seri çarpımsaldır denir.
Triple exponential smoothing (Holt-Winters)
Triple exponential smoothing yöntemi en gelişmiş smoothing yöntemi olarak level (SES), trend, mevsimsellik modellemesi yapabilmektedir.
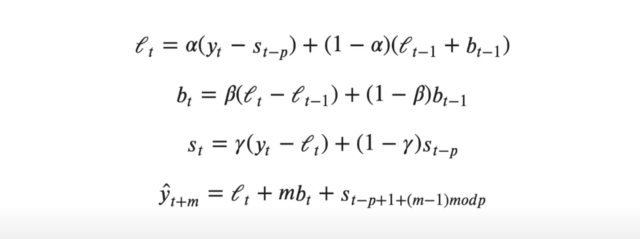
TES yöntemi dinamik olarak level, trend ve mevsimsellik etkilerini değerlendirerek tahmin yapmaktadır. Trend ve/veya mevsimsellik içeren tek değişkenli serilerde kullanılabilir. TES yönteminde tıpkı DES ve SES yöntemlerinde olduğu gibi trend, level ve mevsimsellik bileşenleri için alfa, beta ve gamma ağırlıkları kullanılır.
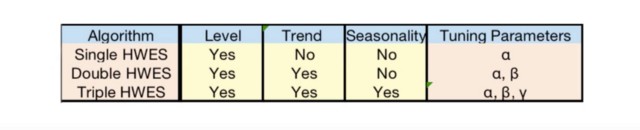
Genel olarak SES, DES ve TES yöntemlerinin tamamına Holt-Winters dendiği görülebilir. Tüm yöntemleri bir arada incelemek amacıyla yukarıda verilen tabloda SES, DES ve TES yöntemlerinin modellemeleri kapsamında içerdikleri zaman serisi bileşenleri ve parametreleri gözlemlenebilir.
Zaman serilerinde istatistiki yöntemler
İstatistiki metotlar kapsamında yaygın kullanılan bazı zaman seri modelleme yöntemleri vardır. Bu yöntemlerden birkaçını inceleyelim:
AR(p): Autoregression yöntemi
Bir zaman serisi kendisinden önceki gecikmelerle tahmin edilir varsayımı üzerinden kullanılır. Trend ve mevsimsellik içermeyen tek değişkenli zaman serileri için uygundur.
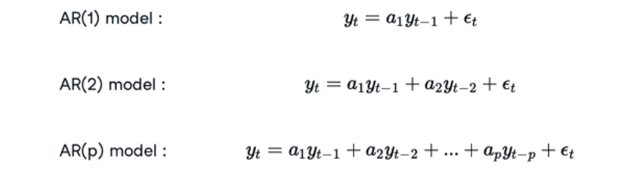
AR(p) yönteminde, önceki zaman adımlarındaki gözlemlerin doğrusal bir kombinasyonu ile tahmin işlemleri yapılır. AR(p) modeli yukarıda gözlemlenebileceği üzere p adet değişkenden oluşur. Buradaki p zaman gecikmesi parametresidir ve bu kapsamda p parametresi arttıkça, geçmiş gerçek değerler daha önceki zaman periyotları üzerinden modele doğrusal formda dahil olacaktır. Örneğin p=1 ise model, bir önceki zaman adımı ile kurulmuş olacaktır.
MA(q): Moving average yöntemi
MA(q) yönteminde önceki zaman adımlarında elde edilen hataların doğrusal bir kombinasyonu ile tahmin yapılır. Trend ve mevsimsellik içermeyen tek değişkenli zaman serileri için uygundur.
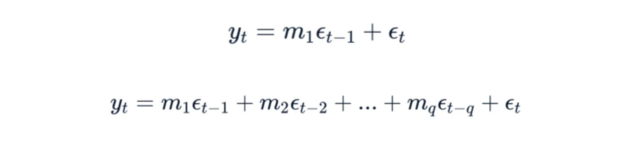
MA(q) modellerinde € değerleri hataları, q zaman gecikmesi sayısını ve m değerleri hataların katsayılarını temsil eder.
ARMA(p,q): AutoRegressive moving average
ARMA(p,q) = AR(p) + MA(q) şeklinde AR ve MA modellerinin birleştirilmesiyle oluşturulur. Geçmiş gerçek değerler ve geçmiş hataların doğrusal bir kombinasyonu ile tahmini yapılır. Trend ve mevsimsellik içermeyen tek değişkenli zaman serileri için uygundur. p, AR modeli ve q, MA modeli için olmak üzere; p ve q zaman gecikmesi sayılarını ifade eder.
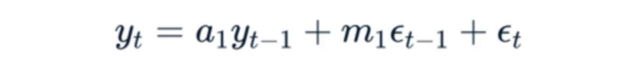
AR(p) modelinde geçmiş gerçek modeller varken, MA(q) modelinde geçmiş hatalar mevcuttur. Bu kapsamda AR(p) ve MA(q) modellerini bir araya getirdiğimiz takdirde SES yöntemine benzer bir model oluşur. Bu model ile SES modeli arasındaki farklar ise SES modelinde var olan iki terimin etkileri, bir alfa değeri ile ağırlıklandırılır. (dolayısıyla SES modelinde alfa değerine ciddi bir bağımlılığı söz konusu olur.) ARMA(p,q) modelinde ise doğrusal bir formda bulunan geçmiş gerçek değerler ve tahmin edilen değerler üzerinden oluşturulan artık değişkenler vardır. Bu değişkenler kapsamında geçmiş gerçek değerlerin katsayısı ve tahmin edilen değerler üzerinden oluşturulan artık değişkenin katsayısı birbirinden bağımsızdır.
Özetle Holt-winters yöntemlerinde terimler bir parametreye göre şekillenirken, ARMA modellerinde terimlerin kendilerine ait katsayıları mevcuttur ve bu katsayılar bulunmaya çalışılır. Veri doğrusal bir formda modellenir ve oluşturulan bu model neticesinde verinin özü öğrenilir.
Holt-Winters yönteminde alfalara dışarıdan verilen değerler üzerinden denemeler gerçekleştirilirken, ARMA yöntemlerinde modellerin içinde yer alan geçmiş gerçek değerler ve hatalara ilişkin katsayılar model aracılığıyla veriden elde edilir.
ARIMA(p,d,q): Autoregressive intregrated moving average
ARIMA(p,d,q) modelinde, önceki zaman adımlarındaki farkı alınmış gözlemlerin ve hataların doğrusal bir kombinasyonu ile tahmin işlemi yapılır. Bir seri durağanlaştırıldığında daha başarılı tahminler yapabilebileceği varsayılır. Bu kapsamda ARIMA yöntemi otomatik bir şekilde fark alma işlemi gerçekleştirerek seriyi durağanlaştırır. Fark alma işlemine örnek olarak, bir zaman aralığındaki değer ile bir önceki zaman aralığındaki değerin farkının alınması verilebilir. Bu kapsamda ARIMA modeli, tek değişkenli, trendi olan fakat mevsimselliği olmayan veriler için uygundur.
p değeri geçmiş gerçek değer gecikme sayısını (otoregresif derece), d değeri fark alma sayısını (fark derecesi), q değeri ise artıklardaki gecikme sayısını başka bir deyişle hata gecikme sayısını (hareketli ortalama derecesini) ifade eder.
SARIMA(p,d,q)(P,D,Q)m: Seasonal autoregressive integrated moving-average
SARIMA yöntemi temelde ARIMA+mevsimsellik olarak betimlenebilir. Trend ve/veya mevsimsellik içeren tek değişkenli serilerde kullanılabilir.
- (p,d,q) ifadeleri ARIMA’dan gelen ifadeler olmak üzere trend elemanlarıdır. ARIMA trendi modelleyebilmekte ama mevsimsellik konusunda zayıf kalmaktaydı.
- (P,D,Q) ise SARIMA’ya ait olan mevsimsel gecikme sayıları olarak, başka bir deyişle seasonal elemanlar olarak betimlenir.
- m değeri ise tek bir mevsimlik dönem için zaman adımı sayısı olmakla birlikte mevsimselliğin görülme yapısını ifade eder.
Dışsal regresörler (SARIMAX) ile mevsimsel otoregresif entegre hareketli ortalama
Mevsimsel otoregresif entegre hareketli ortalama dışsal regresyonlar (SARIMAX), dışsal değişkenlerin modellenmesini de içeren SARIMA modelinin bir uzantısıdır. SARIMAX yöntemi aynı zamanda ARX, MAX, ARMAX ve ARIMAX gibi dışsal değişkenlerle kapsanan durumları modellemek için de kullanılabilir. Yöntem, trend ve/veya mevsimsel bileşenlere ve dışsal değişkenlere sahip tek değişkenli zaman serileri için uygundur.
Vektör otoregresyon hareketli ortalama (VARMA)
Vektör otoregresyon hareketli ortalama (VARMA) yöntemi, bir ARMA modeli kullanarak her zaman serisindeki bir sonraki adımı modeller. ARMA’nın çoklu paralel zaman serilerine genelleştirilmesidir (örneğin çok değişkenli zaman serileri). Yöntem, trend ve mevsimsel bileşenleri olmayan çok değişkenli zaman serileri için uygundur.
Dışsal regresörler (VARMAX) ile vektör otoregresyon hareketli ortalama
Dışsal regresörlü vektör otoregresyon hareketli ortalama (VARMAX), VARMA modelinin dışsal değişkenlerin modellenmesini de içeren bir uzantısıdır. ARMAX yönteminin çok değişkenli bir versiyonudur.
Yukarıda detaylı bir şekilde bahsettiğimiz, zaman serilerinde yaygın olarak kullanılan istatistiksel yöntemleri tek bir tabloda özetyelecek olursak:

Zaman serilerini, kullanım alanlarını ve zaman serilerinde kullanılan çeşitli gelişmiş tekniklerini detaylarıyla inceledik.
Zaman serileri hakkında daha detaylı bilgi edinmek isterseniz Miuul'un Zaman Serileri üzerine oluşturduğu eşsiz eğitimlere mutlaka göz atın. Veri bilimini kariyer yolunuz haline getirmek istiyorsanız, Miuul’un Veri Bilimci Kariyer Yolculuğu tam olarak aradığınız eğitimi sizlere sunacaktır.
Kaynaklar
- Miuul, Zaman serileri
- Wikipedia, Time series
- Towards Data Science, The complete guide to time series analysis and forecasting
- Veri Bilimi Okulu, Python ile zaman serisi analizi
- Veri Bilimi Okulu, Zaman serileri: Geleneksel yöntemler ile yapay sinir ağlarının karşılaştırılması
