Yapay Sinir Ağlarında Öğrenme Süreci: Ağırlıklar, Forward ve Backpropagation

Yapay sinir ağları (Artificial Neural Networks - ANN), günümüz teknolojisinde yaygın olarak kullanılan ve öğrenme süreçleri ile dikkat çeken modellerdir. Bu yazıda, yapay sinir ağlarının öğrenme sürecinin temel adımlarına, ağırlıklar (weights), forward propagation (ileri yönlü yayılım) ve backpropagation (geri yayılım) süreçlerine odaklanacağız. Özellikle ağırlıkların başlatılması ve güncellenmesi aşamaları, ağın performansını doğrudan etkileyen kritik faktörler arasındadır.

Ağırlıklar (Weights) ve Bias Süreçleri

Yapay sinir ağlarındaki her bağlantının önemini belirleyen ağırlıklar, girdi verilerinin her bir özelliği ile çarpılarak nöronlara iletilir. Ağırlıklar, nöronların hangi özelliklere ne kadar önem verdiğini gösterir.

Bias, bir nörona eklenen sabit bir değerdir ve nöronun daha esnek ve doğru çalışmasını sağlayan bir başlangıç değeri olarak işlev görür.

Başlangıç Yöntemleri

Yapay sinir ağlarının öğrenme sürecinde, ağırlıkların ve biasların başlangıç adımları çok önemlidir. Başlangıç için kullanılan yöntemler şunlardır:

• Zero Initialization: Ağırlıkların ve biasların başlangıç değerlerinin sıfır olarak atanması.
• Random Initialization: Ağırlıklar rastgele küçük değerlerle başlatılır, bu da ağın farklı yönlerde keşif yapmasına olanak tanır.
• Xavier Initialization: Ağırlıklar, girdi ve çıktı sayısına bağlı olarak belirlenen bir dağılımdan seçilir, özellikle sigmoid aktivasyon fonksiyonları ile iyi çalışır.
• He Initialization: Özellikle ReLU aktivasyon fonksiyonları için uygundur, ağırlıklar daha büyük bir dağılımdan seçilir.

Başlatma yöntemlerini matematiksel olarak ifade edecek olursak:

• Xavier Başlatma: Ağırlıklar, şu şekilde seçilir:

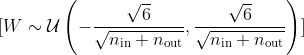
• He Başlatma: Ağırlıklar, şu şekilde seçilir:

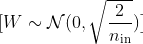
Bu yöntem, özellikle ReLU aktivasyon fonksiyonları için uygundur ve daha büyük bir dağılımdan seçilen ağırlıkları ifade eder.

Doğru başlatma yöntemi, ağın öğrenme sürecini hızlandırarak daha iyi sonuçlar elde edilmesini sağlar. Yanlış bir başlatma ise ağın öğrenme sürecinde tıkanmasına veya sürecin çok yavaş ilerlemesine yol açabilir.

Forward Propagation (İleri Yönlü Yayılım)

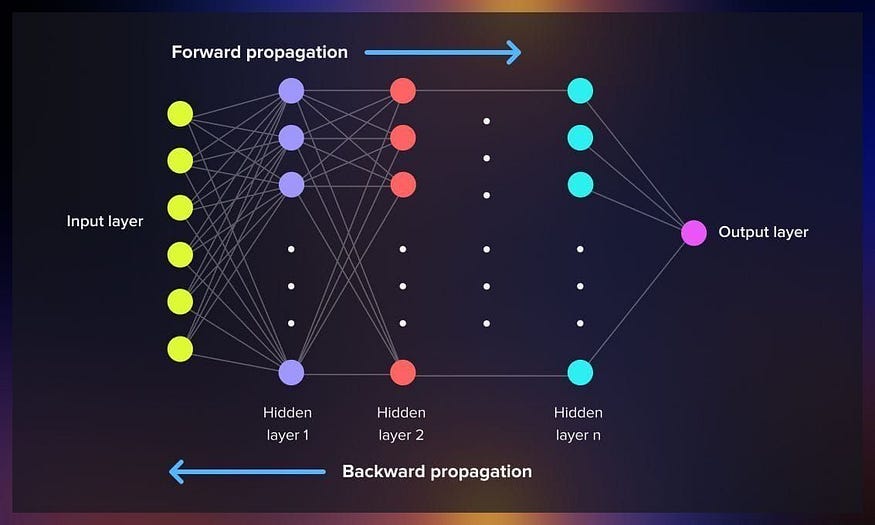
Forward propagation, girdi verilerinin ağ katmanları boyunca ilerleyerek nihai çıktıya dönüştüğü süreçtir. Bu süreçte her bir nöron, ağırlıklar, bias ve aktivasyon fonksiyonları kullanarak hesaplamalar yapar.

Örnek Senaryo:

• Giriş Katmanı (Input Layer): Girdi verilerimiz XXX matrisinde depolanır, örneğin 3 giriş ve 2 eğitim örneği olsun.

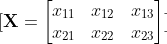
• Ağırlıklar ve Biaslar: Ağırlıklar WWW matrisinde, biaslar ise bbb vektöründe depolanır. Her giriş özelliğinin, çıkış katmanındaki her nörona olan etkisini temsil eder.

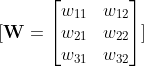
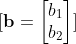
Lineer Kombinasyon ve Aktivasyon:

• Girdi verilerinin ağırlıklarla çarpılması ve biasların eklenmesi sonucu lineer kombinasyon elde edilir.

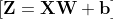
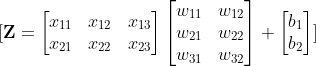
• Elde edilen matris üzerine aktivasyon fonksiyonu uygulanarak nihai çıktı değerleri hesaplanır.

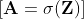
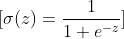
Bu süreç, daha karmaşık ağ yapılarında ve daha fazla katmanda benzer şekilde devam eder, ancak temel prensipler sabittir.

Loss (Kayıp) Fonksiyonunun Hesaplanması

Kayıp fonksiyonu, ağın tahminleri ile gerçek değerler arasındaki farkı ölçer. Yaygın kullanılan kayıp fonksiyonları MSE (Mean Squared Error) ve Cross Entropy'dir. Bu fonksiyonlar, tahmin edilen değerler ile gerçek değerler arasındaki farkları en aza indirgemek için kullanılır.

Bir örnekle açıklayacak olursak:
 

Forward propagation sonucunda elde ettiğimiz çıktı değerleri üzerinden kayıp fonksiyonunu hesaplayabiliriz.

Tahmin edilen değerler : A

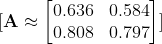
Gerçek değer

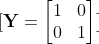
Kayıp fonksiyonu

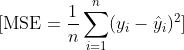
Hesaplama:

Farkların karesi

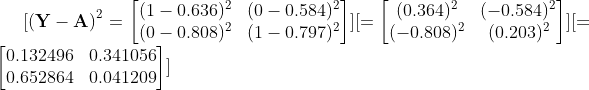
MSE değerini hesaplama

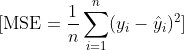
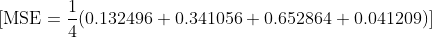
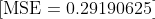
Bu örnekte, MSE kayıp fonksiyonunun değerini hesapladık ve 0.2919 sonucunu bulduk. Bu değer, ağımızın tahminlerinin gerçek değerlerden ne kadar uzak olduğunu gösterir. Kayıp fonksiyonunun değeri ne kadar küçükse, sinir ağımızın performansının o kadar iyi olduğunu söyleyebiliriz.

Tabii ki, farklı problemler veya daha karmaşık ağ yapıları için farklı metodolojiler kullanılabilir. Özellikle kayıp fonksiyonlarının hesaplanmasında çeşitli yöntemler uygulanabilir.

Backpropagation (Geri Yayılım)

Backpropagation, hataları tespit edip, bu hataları minimize etmek amacıyla ağın ağırlıklarını güncelleme sürecidir. Bu süreç, Gradyan Descent ve diğer varyantları gibi optimizasyon algoritmaları ile desteklenir.

Yukarıdaki örnek üzerinden devam edelim:

Aktivasyon Fonksiyon sonuçlarımız(A)

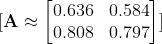
Gerçek değerler(Y)

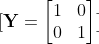
Öncelikle hatamızı hesaplıyoruz.

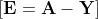
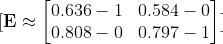
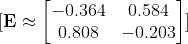
Gradyanların Hesaplanması

Sonraki adımımızda gradyanlar üzerinden loss fonksiyonumuzun çıktılarını ve ağırlıkların güncellenmesi noktasında türev alma yaparak optimizasyon işlemlerine başlıyoruz.

Sigmoid fonksiyonumuz için türev işlemi şu şekilde hesaplanır:

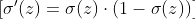
Aktivasyon fonksiyonun türevini hesaplayabilmek için:

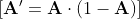
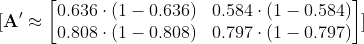
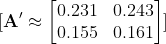
Sonrasında ilk hatamızı aktivasyonumuzun türevi ile çarpıp Delta değerini hesaplıyoruz.

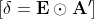
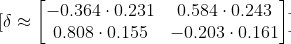
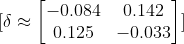
Sonraki adımımızda ağırlıklar güncellenmesi işlemine başlıyoruz.

Ağırlıklar, öğrenme hızı kullanılarak güncellenir. Bu değeri 0.1 olarak işleme başlıyoruz.

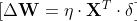
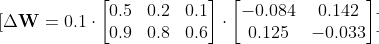
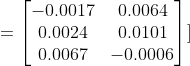
Bu işlem sonucunda yeni güncellenmiş ağırlık değerimiz şu şekilde oluştu.

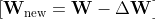
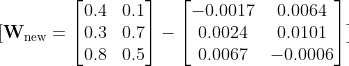
Backpropagation süreci ile ağırlıklar güncellenir. Bu süreç, her iterasyon adımında tekrarlanarak ağın öğrenmesini sağlar. Ağın hata oranı azalır ve model daha doğru tahminler yapabilir hale gelir.

Kaybı minimize etmek için kullandığımız Gradyan Descent optimizasyon algoritmasının farklı varyantları da bulunmaktadır:

• Stokastik Gradyan İnişi (SGD): Her bir örnek için güncelleme yapar.
• Momentum: Güncellemeleri hızlandırmak için önceki adımların yönünü kullanır.
• RMSprop: Her adımın büyüklüğünü dinamik olarak ayarlar.
• Adam: Momentum ve RMSprop’u birleştirerek hızlı ve etkili bir optimizasyon sağlar.

Her optimizasyon algoritması, ağırlıkları güncellemek için farklı yöntemler kullanır. Bu optimizasyon süreçlerine ilişkin detaylı bilgileri bir sonraki içeriğimizde paylaşacağız.

Yapay sinir ağları konusunda daha fazla bilgi edinmek ve öğrenme sürecine dair teknik detayları kavramak için yazımızın faydalı olmasını umuyoruz. Detaylı bilgiler için sitemizi takip etmeye devam edin.