Lojistik Regresyon ve Sınıflandırma Metrikleri
Makine öğrenmesi yöntemlerinden olan lojistik regresyonda genel amaç sınıflandırma problemi için bağımlı ve bağımsız değişkenler arasındaki ilişkiyi doğrusal olarak modellemektir.
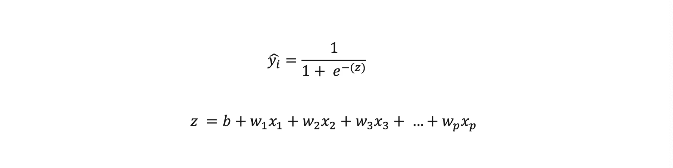
Z doğrusal regresyon denkleminin sonucu Sigmoid fonksiyona yazıldığında, Sigmoid fonksiyonu 0 ve 1 arasında bir olasılık değeri üretir ve bu olasılık değerine göre 1 veya 0 olarak bir sınıf ataması yapılır. Sınıflandırma probleminde her zaman 1 sınıfına ait olma olasılığı hesaplanır.
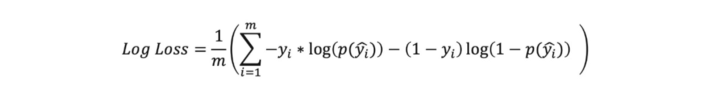
Problem, gerçek değer ile tahmin edilen değerler arasındaki farklara ilişkin, ileride daha detaylı bahsedilecek olan, Log Loss değerini minimum yapabilecek ağırlıkları bulma yöntemiyle çözülür.
Sigmoid fonksiyonu ve bağımlı değişkenin birinci sınıfının gerçekleşme olasılığı
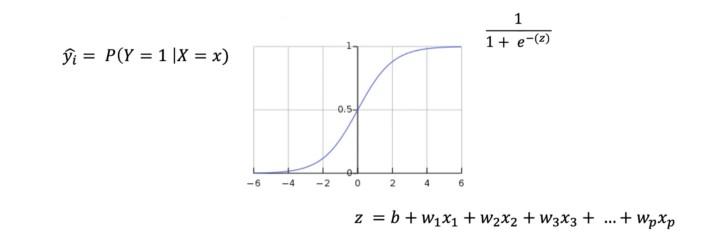
Klasik regresyon yöntemlerinde bağımlı değişkenin 0 ve 1'lerden oluştuğu durumlarda, elde edilen değerlerin 0 ve 1 arasında olması her iş probleminde mümkün olmamaktadır. Sigmoid fonksiyonu tam olarak bu aşamada devreye girerek, z doğrusal formunun değerlerini 0 ve 1 arası değerlere eşlemektedir.
Özetle xᵢ bağımsız değişkenlerinin değerlerine göre Sigmoid fonksiyonu ile yapılan eşleme sonucunda oluşan değerler, bağımlı değişkenin 1. sınıfının gerçekleşmesi olasılığına denk gelir. Örneğin bağımlı değişkenin hayatta kalma durumunu belirten bir değişken olduğu durumda hayatta kalma durumu 1, kalamama durumu ise 0 olarak ifade edilir. Bu işlemin ardından genellikle bir olasılık eşik değeri belirlenir ve bu eşik değerden yüksek değerler 1, düşük değerler ise 0 olarak kabul edilir.
Lojistik Regresyondaki bu dönüşüm işlemi, yapay ve derin öğrenme sınıflandırma problemlerinin temelini oluşturmaktadır.
Lojistik regresyon için gradient descent
Gradient descent (gradyan azalma), rastgele alınan değişkenlerle başlayarak global minimum değerine ulaşmayı amaçlayan en popüler optimizasyon algoritmalarından biridir. Lojistik regresyon kapsamında, gradient descent ile iterasyonlarda kullanılmak üzere cost fonksiyonu üzerinden elde edilen J(θ) değerlerine ulaşılır:
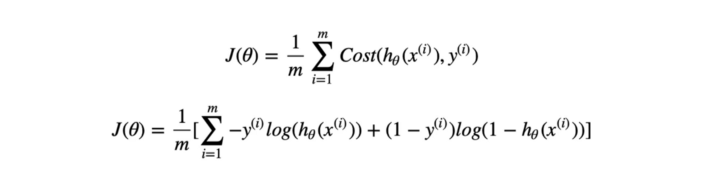
Yukarıdaki formülde hₒ(xᶦ) tahmin edilen değerleri, yᶦ ise gerçek değerleri temsil etmektedir. Bu problem özelinde kayıp fonksiyonu, log loss ifadesidir. Her bir gözlem birimi tek tek gezilerek J(θ) hesaplanır. Log loss fonksiyonu içerisindeki hₒ(xᶦ) ifadesi ise bağımlı değişkenin 1 sınıfının tahmin edilen gerçekleşmesi olasılığıdır. Dolayısıyla -yᶦlog(hₒ(xᶦ)) ifadesi içerisinde değişkenin 1 sınıfının tahmin edilen gerçekleşme olasılığı varken, (1-yᶦ)log(1-hₒ(xᶦ)) ifadesi içerisindeki (1-hₒ(xᶦ)) kısmında 1 sınıfının tahmin edilen gerçekleşmemesi (yani 0 sınıfının tahmin edilen gerçekleşmesi) olasılığı gözlenir.
Ayrıca fonksiyonun yapısı gereği yᶦ gerçek değerleri 0 veya 1 olacağından toplam sembolünün sağındaki ifadelerde ya -yᶦlog(hₒ(xᶦ)) ifadesi ya da (1-yᶦ)log(1-hₒ(xᶦ)) ifadesi sıfır olur.
Bu ifade genel olarak çapraz entropi fonksiyon (cross-entropy loss function) olarak bilinir. Entropi ne kadar yüksek olursa çeşitlilik de o kadar fazla olacaktır. Dolayısıyla gerçek değer ve tahmin edilen değer açısından entropinin düşük, yani çeşitliliğin az olması istenir. Bir sınıfa ait olmanın, tahmin edilen gerçekleşme olasılığı ne kadar yüksekse entropi o kadar düşük olacaktır.
Sonuç olarak gerçek değerler ile gerçek değerlerin gerçekleşmesi olasılığı ifadeleri birbirine ne kadar yakın ise loss değeri (kayıp değeri) o kadar küçük olacaktır.
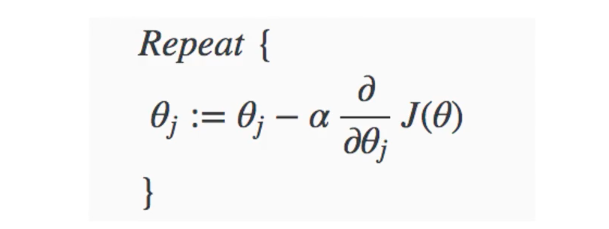
Bir iterasyonda belirli bir ağırlık setinin kullanılması sonucunda, bir hata değeri elde edilir. Ardından cost fonksiyonunun ilgili ağırlıklara göre kısmi türevi alınır. Bu işlem sonucunda elde edilen değerin yönüne göre bu yönün negatifine gidilerek parametrenin değeri güncellenir ve hata değerlerinin düşmesi gözlemlenir.
Sınıflandırma problemlerinde başarı değerlendirme
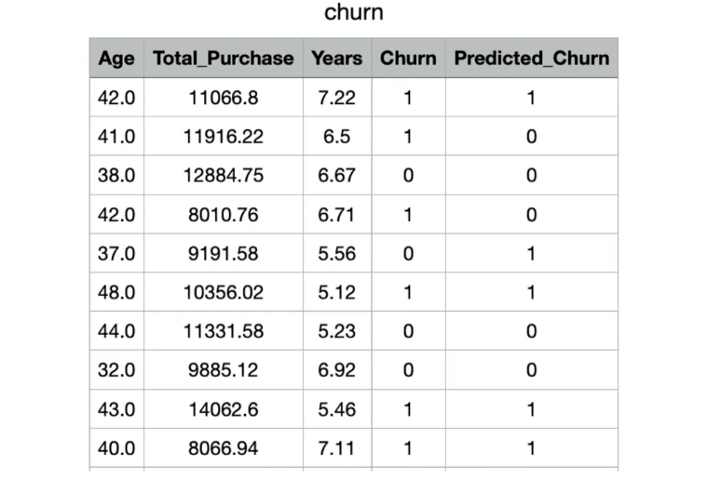
Aşağıdaki örnek müşteri terk veri seti incelendiğinde, müşterilerin terk etme durumu bağımlı değişken olan Churn altında 1 ve terk etmeme durumu 0 ile ifade edilmiştir. Bu kapsamda kurulmak istenen model, özellikleri verilen müşterilerin terk etme/etmeme durumunu tahmin etmek üzerinedir. Bu modelde başarı, ilgili gözlem birimi için tahmin edilen ve gerçek değerin eşleşmesidir.
Bir sınıflandırma modelinin başarısının ölçülebilmesi için çeşitli başarı metrikleri bulunmaktadır. Confusion matrix (karmaşıklık matrisi, accuracy (doğruluk), precision, recall, F1 skoru ve ROC curve (ROC eğrisi) bunlardan bazılarıdır.
Confusion matrix (karmaşıklık matrisi)
Model kurulduktan sonra ortaya çıkan tahmin sonuçlarında tahmin edilen değerlerin gerçek değerler ile eşleştiği gözlem birimleri:
- 1 sınıfı için True Positive (TP)
- 0 sınıfı için True Negative (TN)
Tahmin edilen değerin ve gerçek değerin eşleşmediği gözlem birimleri:
- 1 sınıfı için False Positive (FP) (İstatistikte 1. tip hata olarak betimlenir)
- 0 sınıfı için False Negative (FN) (İstatistikte 2. tip hata olarak betimlenir)
olarak ifade edilir. Yani doğru yapılan işlemlerde True, yanlış yapılan işlemlerde ise False ifadesi kullanılır.
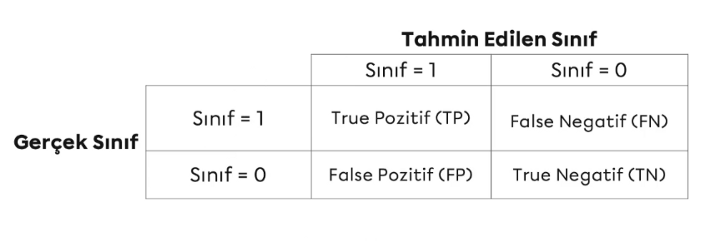
Elde edilen gerçek değerler ile tahmin değerleri karşılaştırmasına göre model başarısı aşağıdaki metrikler ile sayısal olarak ifade edilebilir:
Accuracy (doğruluk)
Doğru sınıflandırma oranıdır. Hesaplamak için (TP+TN)/(TP+TN+FP+FN) formülü kullanılır.
İncelenen sınıflandırma problemi dengeli sınıf dağılımına sahipse (her sınıfta ait benzer sayıda veri bulunuyorsa) accuracy metriği kullanılabilir. Sınıf dağılımının dengesiz olması durumunda, sınıf sayısı düşük olan sınıfı yakalama problemi ile karşılaşılabilmektedir. Sınıf dağılımlarının dengesiz olması durumunda accuracy yerine precision ve recall metrikleri incelenir.
Precision
Pozitif sınıf (1) tahminlerinin başarı oranıdır, yani tahmin edilen pozitif sınıfların (1 olarak tahmin edilen sınıfların) gerçekte ne kadarının pozitif olduğunu gösterir. 1. tip hata ile ilgilenilir. Tahminlerin başarısına odaklanır. Hesaplamak için TP/(TP+FP) formülü kullanılır.
Recall
Pozitif sınıfın (1) doğru tahmin edilme oranıdır. Tahmin edilen pozitif sınıfların ne kadarının doğru tahmin edildiğini gösterir. 2. tip hata ile ilgilenir. Gözden kaçırmaların maliyeti hakkında bilgi verdiğinden önemli bir ölçüdür. Gerçekleri yakalama başarısına odaklanır. Hesaplamak için TP/(TP+FN) formülü kullanılır.
F1 Score
Precision ve recall değerlerinin harmonik ortalamasıdır. Hem Precision hem de Recall değerinin etkisini tutmaktadır. Hesaplamak için 2*(Precision*Recall)/(Precision+Recall) formülü kullanılır.
Sınıflandırmalarda olasılık eşik değeri (classification threshold)
Sınıflandırma modellerinin başarı değerlendirme süreçlerinde, başarı ölçüm metriklerine geçmeden önce, bağımlı değişkenin tahmin edilen değerlerinin elde edilmesi gerekmektedir. Bu kapsamda Sigmoid fonksiyonu kullanılarak ulaşılan olasılık değerlerinin belirlenen bir eşik değerin üstünde veya altında olması durumuna göre tahmin edilen sınıflar belirlenir. Bu eşik değere classification threshold denir.
Bir örnek üzerinde gözlemleyelim:
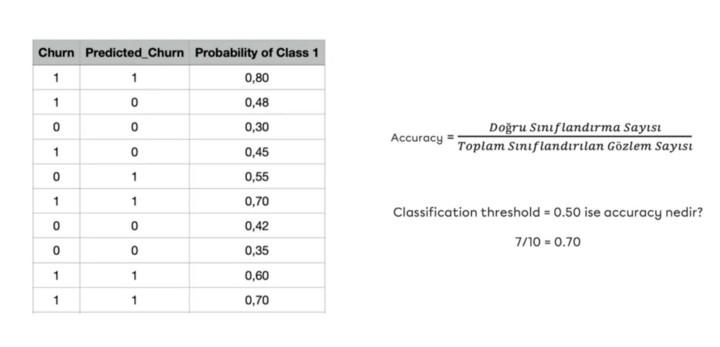
Bu örnekte birinci sınıfın gerçekleşme olasılık değerlerine göre belirlenen 0.50 eşik değeri üzerinden tahmin edilen sınıflar betimlenmiştir. Eşik değerin yükselmesi accuracy değerini düşürecektir. Dolayısıyla hesaplamaların, olası tüm eşik değeri değişimleri göz önüne alınarak yapılması gerekmektedir. Bu problemi çözmek amacıyla sınıflandırma problemlerinde ROC curve yöntemi (receiver operating characteristic curve) kullanılır.
ROC Curve
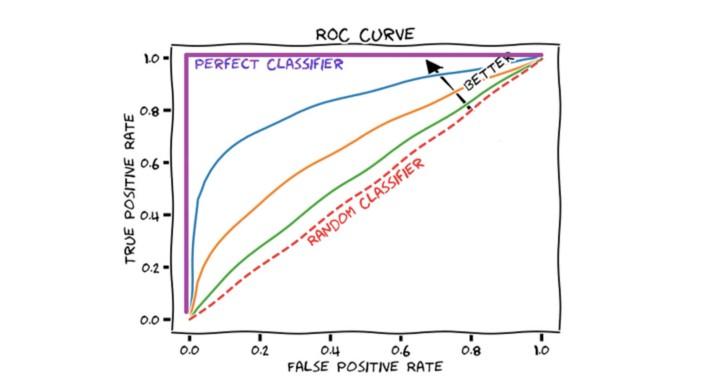
Herhangi bir model kurulmadan, ortalama bir değer tahmin edilmesi durumunda elde edilecek başarının random classifier doğrusu gibi olması beklenir. Random classifier doğrusunun üstünde kalan ROC eğrileri, perfect classifier’a doğru içbükeyleştikçe başarı oranı artmaktadır. Bu eğriler olası eşik değerlere (threshold) göre oluşan karmaşıklık matrisi üzerinden, her bir olası eşik değerine karşılık gelen True Positive ve False Positive değerleri hesaplanarak oluşturulur.
ROC eğrisi ile random classifier arasındaki alana Area Under Curve (AUC) ismi verilmektedir. Bu metrik ROC eğrisinin sayısal bir şekilde ifade edilişidir. AUC, tüm olası sınıflandırma eşikleri için toplu bir performans ölçüsüdür. AUC değerinin yüksek olması sınıflandırmanın iyi yapıldığı anlamına gelir.
Log loss
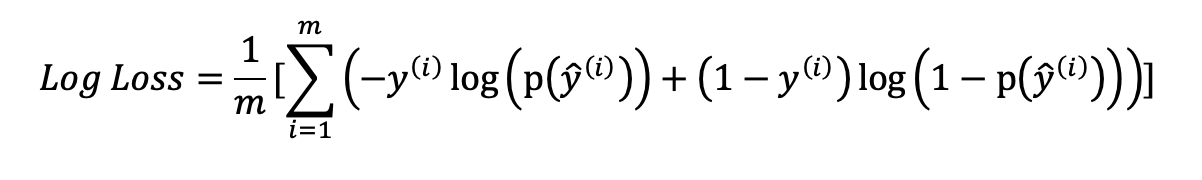 Log loss ifadesi hem modelin başarısı, hem de optimizasyon için değerlendirilen bir metriktir. Hiperparametreler ve ağırlıklar açısından optimizasyon yapmak üzere odaklanılır. Bu metrik cross entropy (çapraz entropi) olarak da isimlendirilir. Entropi bilgi ve çeşitlilik anlamı taşır. Entropi yüksekse bilgi, çeşitlilik ve varyans mevcuttur. Bu nedenle entropinin düşük olması istenir. Log loss üzerinden başarı değerlendirme, entropi özelinde gerçek değerler ile tahmin edilen değerlere ilişkin bir ölçme çabasıdır.
Log loss ifadesi hem modelin başarısı, hem de optimizasyon için değerlendirilen bir metriktir. Hiperparametreler ve ağırlıklar açısından optimizasyon yapmak üzere odaklanılır. Bu metrik cross entropy (çapraz entropi) olarak da isimlendirilir. Entropi bilgi ve çeşitlilik anlamı taşır. Entropi yüksekse bilgi, çeşitlilik ve varyans mevcuttur. Bu nedenle entropinin düşük olması istenir. Log loss üzerinden başarı değerlendirme, entropi özelinde gerçek değerler ile tahmin edilen değerlere ilişkin bir ölçme çabasıdır.
Bu yazı kapsamında sınıflandırma problemlerinin çözümü için kullanılan, en basit makine öğrenmesi yöntemlerden biri olan lojistik regresyon ve başarı ölçüm metriklerine yer verilmiştir. Makine öğrenmesi hakkında detaylı bilgi edinmek için Miuul'un Makine Öğrenmesi üzerine oluşturduğu eşsiz eğitimleri inceleyebilirsiniz. Veri bilimini kariyer yolunuz haline getirmek istiyorsanız, Miuul’un Veri Bilimci Kariyer Yolculuğu tam olarak aradığınız eğitimi sizlere sunacaktır.
Kaynaklar
- Miuul, Makine Öğrenmesi
- Veri Bilimi Okulu, Lojistik Regresyon
- TowardsDataScience, Logistic Regression — Detailed Overview
- ScienceDirect, Logistic Regression
