Python ile Zaman Serisi Analizi 3.Bölüm - Python Kullanarak Zaman Serisi Analizinde İstatistiksel Yöntemler
İstatistiksel yöntemler, zaman serisi verilerini analiz etmek ve tahmin etmek için güçlü birer araçtır. Zaman serilerinde kullanılan beş istatistiksel yöntem şunlardır:
* Oto Regresyon (AR),
*Hareketli Ortalama (MA),
*Otoregresif Hareketli Ortalama (ARMA),
*Otoregresif Entegre Hareketli Ortalama (ARIMA),
*Mevsimsel Otoregresif Entegre Hareketli Ortalama (SARIMA).
Bu modeller, zaman serisi davranışının matematiksel temsilleridir ve gelecekteki değerleri tahmin etmek için kullanılabilir.
Oto Regresyon (Auto Regression — AR(p)) :
Bir zaman serisinin mevcut değerinin önceki değerlerden etkilendiği fikrine temellendirilir. Mevcut değer ile geçmiş değerler arasında bir ilişki olduğunu varsayarak, zaman serisinin geçmiş değerlerinin doğrusal bir fonksiyonu ile tahmin yapılır.
Aşağıdaki formülde görüldüğü gibi AR(p) modelinde p zaman gecikmesi sayısıdır. p parametresinin değeri arttıkça geçmiş değerler, bir önceki zaman periyotları üzerinden modele doğrusal olarak dahil edilir.
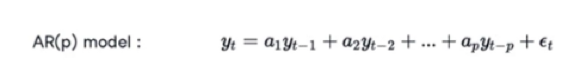
Trend ve mevsimsellik içermeyen tek değişkenli zaman serileri için uygundur.
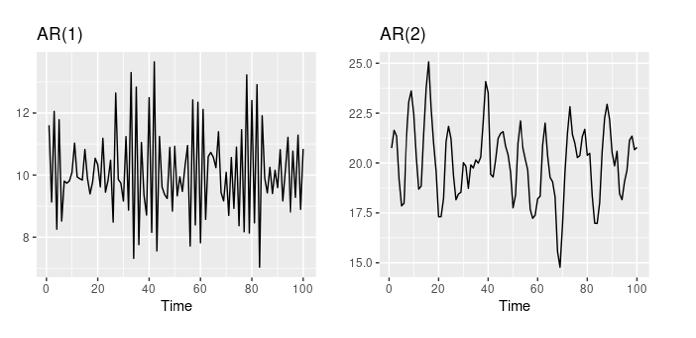
AR modellerinin temel avantajı, geçmiş değerleri hesaplayarak zaman serisi dinamiklerini anlama yeteneğidir. Ancak, AR modellerinin bazı sınırlamaları vardır. Bunlardan biri, mevcut ve geçmiş değerler arasındaki doğrusallık varsayımıdır. Bu her zaman böyle değildir. Ayrıca, doğru tahminler yapmak için büyük miktarda veri gerekir.
Hareketli Ortalama (Moving Average — MA(q)) :
Hareketli ortalama (MA) modeli, zaman serisi analizinde yaygın olarak kullanılan istatistiksel bir modeldir. Bu model, geçmiş hataların tahmindeki bir zaman serisinin gelecekteki değerini etkilediği fikrine dayanmaktadır.
Önceki zaman adımlarında elde edilen hataların doğrusal bir kombinasyonu ile tahmin yapılır.
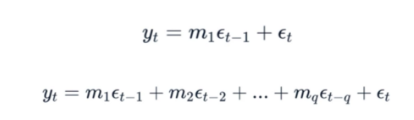
MA(q) modelinde, hataların katsayıları m, hata terimleri ε ve zaman gecikmesi sayısı q'dir. Model, tarihsel veriler üzerinde eğitilir ve en küçük kareler yöntemi kullanılarak katsayılar belirlenir. Model daha sonra zaman serisi verilerinin gelecekteki değerlerini tahmin etmek için kullanılabilir.
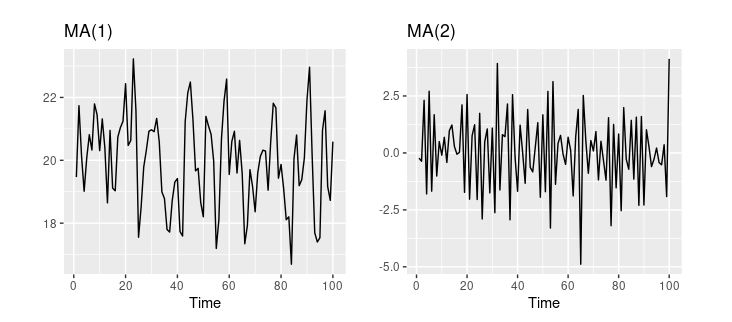
MA modellerinin temel avantajı, beklenmeyen olayların ve hataların zaman içindeki etkisini anlama yeteneğidir. Ancak, MA modellerinin bazı sınırlamaları vardır. Bunlar, doğrusallık varsayımları ve büyük miktarda veriye duyulan ihtiyaçtır. Trend ve mevsimsellik içermeyen tek değişkenli zaman serileri için uygundur.
Otoregresif Hareketli Ortalama (AutoRegressive Moving Average — ARMA(p, q) = (AR(p) + MA(q)) :
ARMA(p,q) modeli, AR(p) ve MA(q) modellerinin özelliklerini birleştirir. AR(p) modeli geçmiş gerçek değerleri, MA(q) modeli ise geçmiş hataları kullanır. p ve q, zaman gecikmesi sayılarını temsil eder. ARMA(p,q) modeli, geçmiş gerçek değerlerin doğrusal bir kombinasyonunu ve tahmin edilen değerlerden elde edilen artık değişkenleri kullanır. Geçmiş gerçek değerlerin katsayısı ile tahmin edilen değerlerden elde edilen artık değişkenin katsayısı, birbirinden bağımsız parametrelerdir.
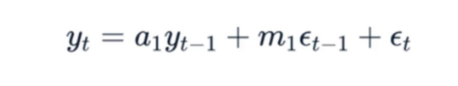
Yani ARMA, geçmiş gerçek değerler ve geçmiş hataların doğrusal bir kombinasyonuna dayalı olarak geliştirilen modeldir. Trend ve mevsimsellik içermeyen tek değişkenli zaman serileri için uygundur.
Otoregresif Entegre Hareketli Ortalama ARIMA(p,d,q) (Autoregressive Integrated Moving Average) :
AR(p), MA(q) ve ARMA(p,q) modelleri, durağan zaman serileri için iyi çalışan yöntemlerdir. Ancak, çoğu zaman serisi, bir trend veya mevsimsellik gibi durağanlığı bozan faktörler içerdiğinden durağan değildir.
Zaman serileri, fark alma yöntemi kullanılarak durağan hale getirilebilirler. Fark alma yöntemi, mevcut zaman adımını önceki zaman adımından çıkararak elde edilen farkı kullanarak zaman serisini durağan hale getirmeyi amaçlar. Zaman serisinin fark alınmış değerlerinin ve tahmin edilen hataların doğrusal bir kombinasyonu ile tahmin yapılır. Tek değişkenli, trendi olan ancak mevsimselliği olmayan veriler için kullanılabilir.

Burada p, geçmiş gerçek değer gecikme sayısı; d, fark işlemi sayısı (fark derecesi) ve q hata gecikme sayısını (hareketli ortalama derecesi) tmesil etmektedir.
ARIMA modellerinin en önemli avantajı, trendleri ve mevsimsel bileşenleri zaman serilerinde yakalama yetenekleridir. Durağan olmayan zaman serileriyle başa çıkmaya izin verir ve tahmin doğruluğunu iyileştirmek için standart istatistiksel tekniklerle birlikte kullanılabilir. Bununla birlikte, doğrusallık varsayımları nedeniyle büyük miktarda veri gerektirir.
Mevsimsel Otoregresif Entegre Hareketli Ortalama SARIMA(p,d,q)(P,D,Q)m (Seasonal Autoregressive Integrated Moving Average):
SARIMA modeli, ARIMA modelindeki mevsimsel olmayan bileşenlere (p,d,q) ek olarak, mevsimsel bileşenlere (P,D,Q,m) sahiptir. Trende ve/veya mevsimselliğe sahip tek değişkenli serilerde kullanılabilir.
p, d ve q, ARIMA modelinden gelen parametrelerdir ve trend elemanlarıdır.
p: gerçek değerlerin otoregresif derecesidir.
d: fark işleminin derecesidir.
q: hata terimlerinin hareketli ortalama derecesidir.
p, d ve q, mevsimsel gecikme sayılarıdır. Mevsimsellik elemanlarıdır. m, mevsimsellik döneminin uzunluğudur ve mevsimselliğin yapısını ifade eder.
İstatistiki yöntemler kullanılacağı zaman aşağıdaki tablo yardımı ile karar verilebilir:
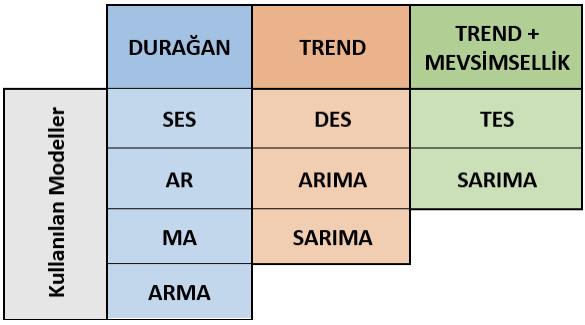
İstatistiksel yöntemlerin kullanım avantajları şu şekilde sıralanabilir:
- Birçok istatistiksel yöntem, basit matematiksel formüllere dayanır ve anlaşılması ve açıklanması kolaydır. Bu nedenle, sonuçların yorumlanması ve karar vermek için kullanılması kolaydır.
- İstatistiksel yöntemler, verilerdeki aykırı değerlere ve diğer gürültü biçimlerine karşı dayanıklı olacak şekilde tasarlanabilir. Bu nedenle, sağlam yöntemlerdir.
- Birçok istatistiksel yöntem hesaplama açısından verimlidir. Bu nedenle, büyük ve karmaşık zaman serisi veri kümelerini analiz etmek mümkündür.
Bu kadar övdükten sonra biraz da zayıf yönlerinden bahsedelim:
- Birçok istatistiksel yöntem, pratikte karşılanamayan durağanlık, doğrusallık ve normallik gibi kritik veri özellikleri hakkında varsayımlarda bulunur.
- Bazı istatistiksel yöntemler, doğru sonuçlar elde etmek için büyük miktarda veri gerektirir. Verilerin sınırlı veya kalitesiz olması, hatalı sonuçlar elde etmemize neden olur.
- İstatistiksel yöntemler geçmiş gözlemlere dayanır ve geçmiş verilere dahil olmayan gelecekteki olayları yakalayamaz. Bu nedenle, sınırlı doğruluğa sahiptir.
- İstatistiksel modellerin her birinin güçlü ve zayıf yönleri vardır ve uygun modelin seçilmesi, zaman serisi verilerinin özelliklerine ve yapacağımız analizin amacına bağlıdır.
Ayrıca istatistiksel yöntemlerin zaman serisi analizine yönelik tek yaklaşım olmadığına dikkat etmek önemlidir. Diğer yöntemleri ve modelleri de dikkate almak her zaman faydalı olacaktır. Zaman serileri hakkında daha fazla bilgi edinmek ve sektörden uygulamalar yapmak isterseniz Miuul’ un zaman serileri eğitimine göz atabilirsiniz.
Kaynaklar
Veri Bilimi Okulu, Python ile zaman serisi analizi
simpli learn, A complete guide to get a grasp of time series analysis
Analytics Vidhya, Learning time series analysis & modern statistical models
Otexts, Moving average models
