Python ile Zaman Serisi Analizi 2. Bölüm - Zaman Serisi Analizinde Smoothing Yöntemleri

Zaman serisi verilerini tahmin ederken amaç, gözlem dizisinin gelecekte nasıl devam edeceğini tahmin etmektir. Zaman serilerinde aşağıdaki belli başlı yöntemleri kullanıp, tahmin başarısı en yüksek olan yöntemle modellemeye gidilmektedir.

Zaman serisi analizinde smoothing (düzeltme) yöntemleri

Verilerdeki gürültüyü azaltmak, trendleri veya desenleri daha iyi ortaya çıkarmak için kullanılan istatistiksel tekniklerdir, Holt-Winters de denilir.

Hareketli ortalama (moving average): Belirli bir zaman aralığındaki verilerin aritmetik ortalamasını alarak verilerdeki dalgalanmaları düzleştiren bir yöntemdir. Trendi gözlemlemek için ya da feature türetiminde kullanılabilir.

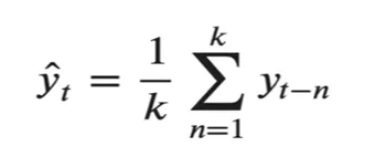
Zaman serisi teorisine göre, zaman serisi en çok kendisinden bir önceki değerden etkilenir. Hareketli ortalama formülünden anlaşılacağı üzere gelecek değer, kendisinin k adet önceki değerinin ortalamasıdır.

Ağırlıklı ortalama (weighted average): Hareketli ortalamaya benzer olmakla beraber son verilere daha fazla ağırlık veren bir yöntemdir. Gerçek değerlere hareketli ortalamaya göre daha başarılı yaklaşır.

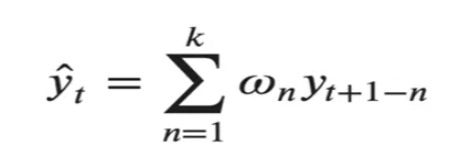
Zaman serisinin trendi ve mevsimselliğinin olmaması durumunda tahmin için kullanılacak en iyi yöntem ağırlıklı ortalamadır.

Single exponential smoothing (SES/Single HWES): Basit Üstel Düzeltme Yöntemi olan SES, sadece durağan serilerde başarılıdır, trend ve mevsimselliği modelleyemez. Geçmiş değerlere daha fazla ağırlık vererek üstel düzeltme yapar. Gelecek, yakın geçmişten daha çok etkilenir varsayımıyla geçmişin etkileri ağırlıklandırılır.

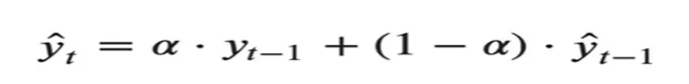
α; 0 ile 1 arasında bir değer alan smoothing faktördür ve değere ne kadar ağırlık verileceğini belirler. Geçmiş gerçek değer (learning) ile geçmiş tahmin edilen değerlerin (remembering) üstel olarak ağırlıklandırılmasıyla tahmin yapılır.

Doble exponential smoothing (DES/Double HWES): Çift Üstel Düzeltme yöntemi DES; SES yönteminin yaptığına ek olarak trend etkisini de göz önünde bulundurur ve üstel düzeltme yapar. Ancak mevsimselliği modelleyemez.

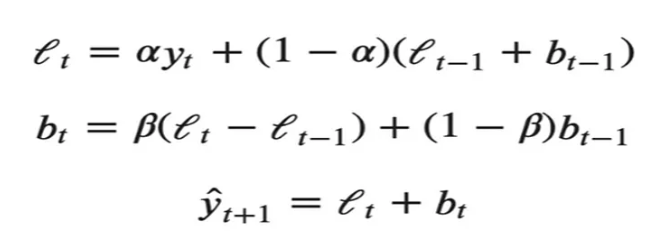
İlk formül level’i, ikinci formül ise trendi ifade eder. α parametresi level’a ilişkin geçmiş değer ve tahmin edilen değeri ne kadar ağırlıklandıracağımızla ilgiliydi. DES, α parametresine ek olarak trend bileşenine ilişkin optimize edilmesi gereken parametre olan β’yı da kullanır.

Triple exponential smoothing (TES/Triple HWES): Winters Üstel Düzeltme Yöntemi, DES yönteminin yaptığına ek olarak mevsimselliği de modeller. En gelişmiş smoothing yöntemidir.

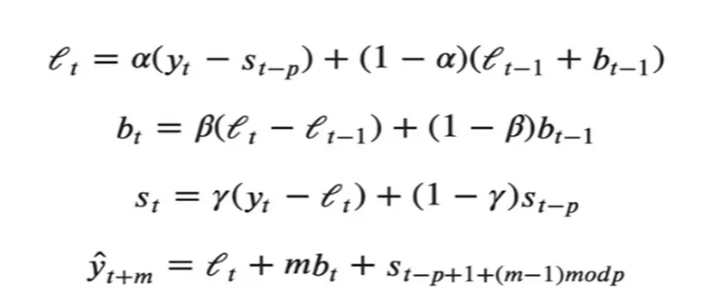
Level ve trend’e ek olarak 3.formül mevsimselliği ifade eder. Burada ꝩ, mevsimsellik bileşenine ilişkin optimize edilmesi gereken parametredir.

Bu yöntem ile dinamik olarak level, trend ve mevsimsellik etkilerini değerlendirerek tahmin yapılmasına olanak sağlar.

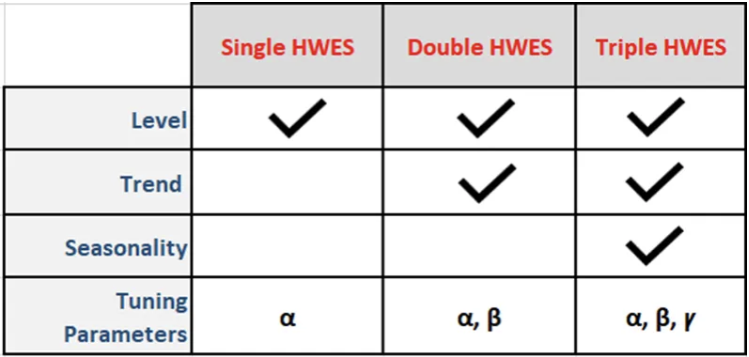
Şimdi bir tablo yardımıyla yöntemleri kıyaslayarak öğrendiklerimizi pekiştirelim ardından bir zaman serisi örneğinde uygulayalım.

Zaman serisi problemi 

Amerika’da Mart 1958 — Aralık 2001 yılları arasında ölçülmüş, atmosferdeki karbondioksit miktarının gözlem verilerinden faydalanarak bir hava kirliliği tahmin modeli oluşturalım.

Öncelikle kullanılacak kütüphaneyi import edelim;

import statsmodels.api as sm

Adım 1: Veri setinin okutulması ve basit düzenlemelerin yapılması.

data = sm.datasets.co2.load_pandas()
y = data.data # hedef değişken

# Hafatalık formattan aylık formata çevirelim:
y = y['co2'].resample('MS').mean()

y
1958–03–01 316.100000
1958–04–01 317.200000
1958–05–01 317.433333
1958–06–01 NaN
1958–07–01 315.625000
… 
2001–08–01 369.425000
2001–09–01 367.880000
2001–10–01 368.050000
2001–11–01 369.375000
2001–12–01 371.020000

Serinin bir grafiğini çizdirip bileşenlerini inceleyelim:

y.plot(figsize=(15,6))


plt.show()

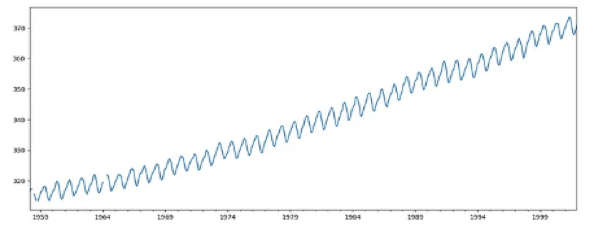
                                                        Zamana bağlı ölçülen Karbondioksit miktarı grafiği

Grafiği incelediğimizde “trend ve mevsimsellik vardır, durağan değildir” yorumlarını yapabiliriz.

Veri setimizi zaman bileşenlerine ayıralım:

def ts_decompose(y, model="additive", stationary=False):
    result = seasonal_decompose(y, model=model)
    fig, axes = plt.subplots(4, 1, sharex=True, sharey=False)
    fig.set_figheight(10)
    fig.set_figwidth(15)

    axes[0].set_title("Decomposition for " + model + " model")
    axes[0].plot(y, 'k', label='Original ' + model)
    axes[0].legend(loc='upper left')

    axes[1].plot(result.trend, label='Trend')
    axes[1].legend(loc='upper left')

    axes[2].plot(result.seasonal, 'g', label='Seasonality & Mean: ' + 
    str(round(result.seasonal.mean(), 4)))
    axes[2].legend(loc='upper left')

    axes[3].plot(result.resid, 'r', label='Residuals & Mean: ' + 
    str(round(result.resid.mean(), 4)))
    axes[3].legend(loc='upper left')
    plt.show(block=True)

    if stationary:
        is_stationary(y)

ts_decompose(y, stationary=True)

Çıkan grafiğimizi inceleyelim:

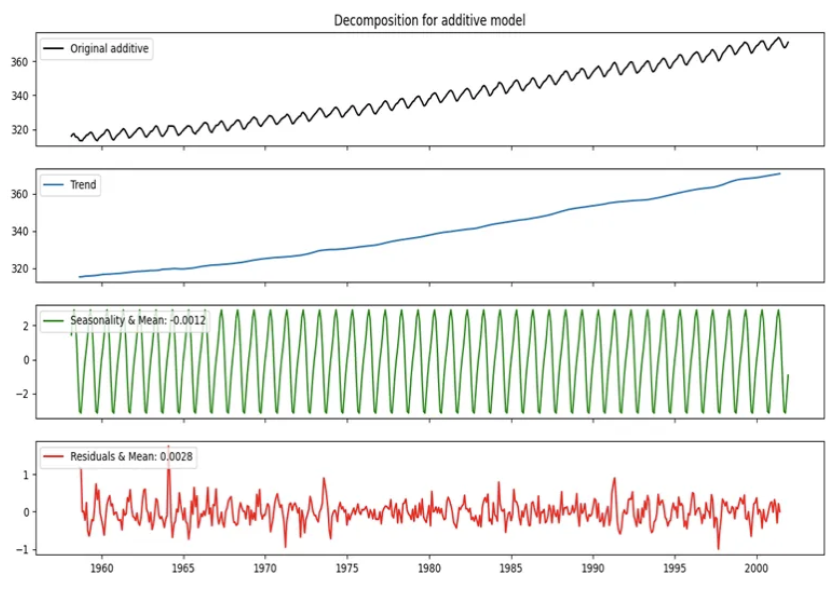
                                                                               Zaman serisinin bileşenleri

Birinci grafikte serinin level ortalama değerlerini, ikinci grafikte yukarı yönlü artan trendi, üçüncü grafikte mevsimselliğin olduğunu, dördüncü grafikte ise artıkların (hataların) ortalaasının 0’ın etrafında toplandığını gözlemleyebiliriz. Son olarak serinin durağan olmadığını kod çıktısından okuruz (Result: Non-Stationary (H0: non-stationary, p-value: 0.999)).

Adım 2: Smoothing yöntemlerini uygulamak ve 1 aylık tahmin için minimum hatayı yakalamaya çalışmak.

Serinin bileşenlerine baktığımızda trend ve mevsimselliğin olduğunu gözlemlemiştik. Bu nedenle Triple Exponential Smooting (Holt-Winters) yöntemini uygulayıp elde ettiğimiz hatayı inceleyelim.

Zaman serileri toplamsal ya da çarpımsal olabilmektedir.

y(t) = Level + Trend + Seasonality + Noise (Toplamsal model)
y(t) = Level * Trend * Seasonality * Noise (Çarpımsal model)

Seriyi çarpımsal ve toplamsal olarak hesaplayıp en düşük hatayı veren modeli seçeriz. Hesaplamaların sonucunda, toplamsaldaki hata çarpımsal modeldekinden daha düşük çıktığı için “trend=add” ve “seasonal=add” diyerek işlemlerimize toplamsal modelden üzerinden devam edebiliriz.

Mevsimsellik periyodu aylık periyod olduğundan “seasonal_periods=12” olacaktır. “smoothing_level” (level) , “smothing_slope” (trend) ve “smoothing_seasonal” (mevsimsellik) değerlerini 0.5 olarak seçelim.

tes_model = ExponentialSmoothing(train,
                                                                      trend="add",
                                                                      seasonal="add",
                                                                      seasonal_periods=12).fit(smoothing_level=0.5,
                                                                      smoothing_slope=0.5,
                                                                      smoothing_seasonal=0.5)

y_pred = tes_model.forecast(48)
plot_co2(train, test, y_pred, "Triple Exponential Smoothing")

Çıkan grafiğimizi inceleyelim:

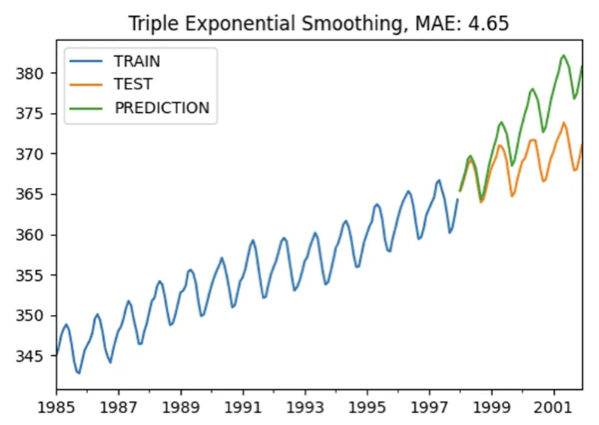
Modelimizi kurduğumuzda level, trend ve mevsimselliğin biraz da olsa yakalandığını görmekteyiz. Ortalama mutlak hata (MAE, Mean Absolute Error) değeri 4.65 olarak hesaplanmıştır.

Adım 3: Hiparparametre optimizasyonu ile hatanın düşürülmesi.

alphas = betas = gammas = np.arange(0.20, 1, 0.10)

abg = list(itertools.product(alphas, betas, gammas))

ef tes_optimizer(train, abg, step=48):
    best_alpha, best_beta, best_gamma, best_mae = None, None, None, float("inf")
    for comb in abg:
        tes_model = ExponentialSmoothing(train, trend="add", seasonal="add", seasonal_periods=12).\
            fit(smoothing_level=comb[0], smoothing_slope=comb[1], smoothing_seasonal=comb[2])
        y_pred = tes_model.forecast(step)
        mae = mean_absolute_error(test, y_pred)
        if mae < best_mae:
            best_alpha, best_beta, best_gamma, best_mae = comb[0], comb[1], comb[2], mae
        print([round(comb[0], 2), round(comb[1], 2), round(comb[2], 2), round(mae, 2)])

    print("best_alpha:", round(best_alpha, 2), "best_beta:", round(best_beta, 2), "best_gamma:", round(best_gamma, 2),
          "best_mae:", round(best_mae, 4))

    return best_alpha, best_beta, best_gamma, best_mae

best_alpha, best_beta, best_gamma, best_mae = tes_optimizer(train, abg)

En düşük hatayı veren alfa beta ve gama değerlerinin aşağıdaki gibi olduğunu görürüz:

                                                                   best_alpha: 0.8

                                                                   best_beta: 0.5

                                                                   best_gamma: 0.7

                                                                   best_mae: 0.6177

Adım 4:En uygun parametreleri kullanarak modelin yeniden kurulması

final_tes_model = ExponentialSmoothing(train, trend="add", seasonal="add", seasonal_periods=12).\
            fit(smoothing_level=best_alpha, smoothing_trend=best_beta, smoothing_seasonal=best_gamma)

y_pred = final_tes_model.forecast(48)

plot_co2(train, test, y_pred, "Triple Exponential Smoothing")

Çıkan grafiğimizi inceleyelim:

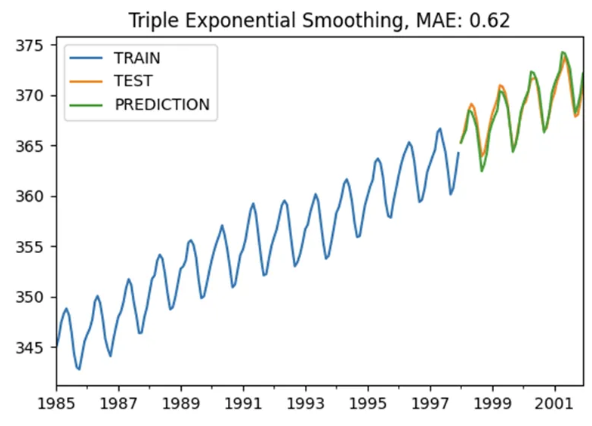
Modelin, trendi ve mevsimselliği 0.62 MAE ile iyi bir düzeyde tahminleyebildiğini görmekteyiz.

Bu yazımızda örnek bir uygulama üzerinden bir serinin özelliğini dikkate alarak seçmiş olduğumuz smoothing yöntemine ile zaman serisi analizi yaptık ve tahminde bulunduk. MAE değerini hiperparametre optimizasyonu ile düşürerek serinin trendini ve mevsimselliğini yakaladık. Zaman serileri hakkında daha fazla bilgi edinmek ve uygulamalar yaparak kendinizi bir adım ileriye götürmek isterseniz Miuul’un sunmuş olduğu Zaman Serileri eğitimini inceleyebilirsiniz.

Kaynaklar

Veri Bilimi Okulu, Python ile zaman serisi analizi

Simplilearn, A complete guide to get a grasp of time series analysis

Analytics Vidhya, Learning time series analysis & modern statistical models