Merkezi Eğilim Ölçüleri Nelerdir?

Bir araştırmacının bir proje sürecinde nihai sonuç elde edebilmesi için üzerinde çalıştığı veri setinde bulunan gözlemlerden bilgi edinmesi gerekir. Veri setinde yer alan gözlemlerin sayısı arttıkça bilgi edinmek zorlaşır. Bu sebeple verileri özetlemek ve veriler hakkında genel bir bilgiye sahip olmak için birtakım istatistiki araçlar kullanılır. Ancak veri setini tanımaya çalışırken her ne kadar ilk etapta grafik ve frekans tablolarından yararlansak da bu araçlar yeterli olmayabilir. 

Veri setini anlamak için görsel nitelikteki araçların yanı sıra sayısal verilere de ihtiyaç duyarız. Tanımlayıcı istatistik alanının ilgilendiği nicel değişkenlere ilişkin gözlemlerin incelendiği bu ölçütlere merkezi eğilim ve dağılım ölçüleri denir. Bu yazımızda merkezi eğilim ölçülerinden bahsedeceğiz.

Merkezi eğilim ölçüleri

Kitleye ilişkin verilerin odaklaşma noktasını özetleyen ölçüleri barındırır. Yalnızca tek bir değer alırlar. Kısaca, bir veri kümesinin merkez noktasının değerini temsil eden istatistiki özet olarak tanımlanabilir. 

En çok kullanılan merkezi eğilim ölçüleri; aritmetik ortalama, medyan (ortanca), mod (orta değer), geometrik ortalama ve harmonik ortalamadır.

Aritmetik ortalama

Bir veri kümesinin merkezinin açıklanması için en çok kullanılan, tüm gözlemlerin toplanarak gözlem sayısına bölünmesiyle elde edilen değerdir. En sık kullanılan ölçüt olsa da veride yer alan aykırı gözlemlere toleransı düşük bir ölçüttür. Eşit aralıklı ve oran ölçek düzeyinde ölçülen değişkenler için kullanılmakta olup hem kitle hem örneklem için hesaplanır.

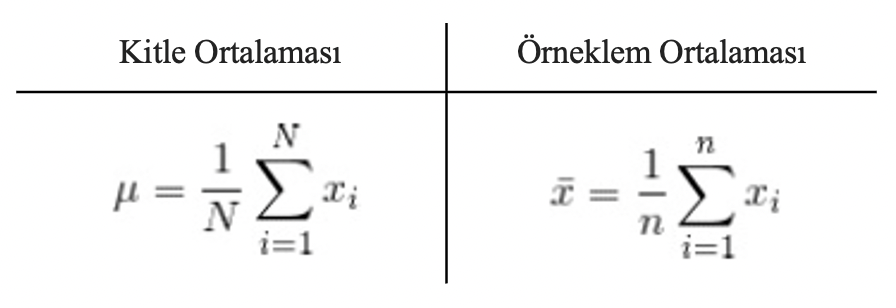
Burada;

• μ : kitleye ilişkin aritmetik ortalamayı,
• x : örnekleme ilişkin aritmetik ortalamayı,
• N : Kitlenin toplam gözlem sayısını,
• n  : Örneklemin toplam gözlem sayısını ve
• xi : i. gözlem değerini temsil etmektedir.

Aritmetik ortalama hesaplanırken karşılaşılan bazı özel durumlar mevcuttur. Bunlardan biri, gözlemlerin bazı değerlerinin farklı frekanslarla tekrarlaması durumudur. Bu durumda ortalama hesaplanırken gözlemlerin frekansları da göz önünde bulundurulur. Bunlara sınıflandırılmış aritmetik ortalama da denilmekte ve aşağıdaki şekilde hesaplanmaktadır:

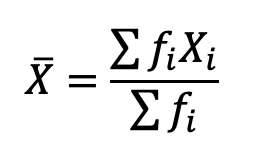
Bir diğer özel durum ise; her değişkenin etkisinin aynı derecede olmaması durumudur. Böyle bir durumda değişkenlerin her birine ağırlık atanarak ortalama hesabı yapılır ve hesaplanan değere gruplandırılmış aritmetik ortalama ismi verilir:

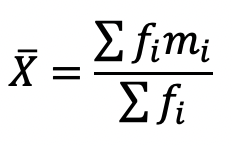
Medyan (Orta değer, ortanca)

Medyanın tanımına geçmeden önce asimetrik ve simetrik dağılım kavramlarına değinelim.

Bir veri setinde yer alan gözlemler küçükten büyüğe doğru sıralandığında en ortada yer alan değere Medyan değeri adı verilmektedir. Aykırı gözlemlere, aritmetik ortalamaya göre daha dayanıklıdır. Bu sebeple asimetrik dağılıma sahip veri setlerinde merkezin hesaplanmasında oldukça iyi bir ölçüttür. Sınıflama ölçme düzeyi hariç diğer ölçme düzeylerinde kullanılmaktadır.

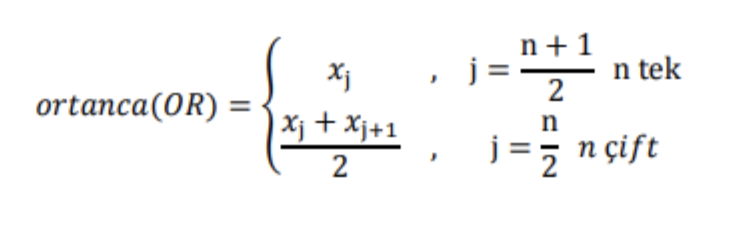
Elimizde bir grup öğrencinin olduğunu ve bu öğrencilerin boy uzunluklarına ilişkin gözlem değerlerimizin aşağıdaki gibi olduğunu düşünelim:

172, 154, 185, 163, 156, 187, 179, 192, 186

Elimizde toplam 9 gözlem bulunmaktadır.  Değerleri önce küçükten büyüğe doğru sıralanırsa:

154, 156, 163, 172, 179,  185, 186, 187, 192

Burada ortanca değer; n=9 tek sayı iken (9+1)/2 = 5. gözlem değeri olan 179 değeridir.

Mod (Tepe değer)

Bir veri seti içerisinde en çok tekrarlanan gözlem değerine mod (tepe değer) ismi verilir. Değerlerin küçükten büyüğe sıralanması şart değildir ama sıralandığı zaman tepe değere daha kolay ulaşılır. Bazı dağılımlarda mod birden çok değer olabilmektedir. Bazen de mod, dağılımı yansıtmayabilir. 

Diyelim ki elimizde bir grup öğrencinin ağırlıklarına ilişkin gözlemler olsun:

56, 57, 57, 58, 72, 72, 72, 80, 81, 82

Burada görülebileceği üzere tepe değeri (mod) en çok tekrar eden değer olan 72’dir.

Geometrik Ortalama

Çalışmalarda bazı durumlarda değişkenlerin orijinal değerleri yerine logaritmaları veya tersleri için hesaplama yapılır. Bu durum, gözlemin bir önceki gözleme bağlı olarak değişmesi ve bu değişimin hızının belirlenmek istendiği durumdur.

Geometrik ortalamanın kullanılamadığı durumlar mevcuttur. Herhangi bir gözlemin sıfır veya negatif değerli olması durumunda geometrik ortalama hesaplanamaz. Aritmetik ortalamadan küçüktür ve uç değerler açısından aritmetik ortalamadan daha toleranslıdır. 

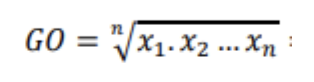
Burada,

• Xi : i. gözlem değerini temsil etmektedir.

Harmonik ortalama

Gözlem değerlerinin terslerinin aritmetik ortalamasının tersi olarak ifade edilir. Genellikle oranların ortalamasının istendiği durumlarda kullanılır.

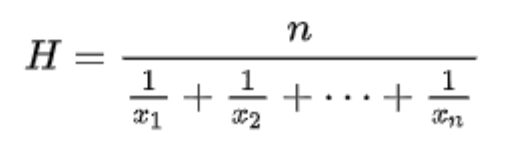
Aritmetik ortalama - mod - medyan arasındaki ilişki 

Aritmetik ortalama, mod ve medyan arasındaki ilişki durumuna göre veri setinin dağılım durumu hakkında fikir sahibi olunabilmektedir.

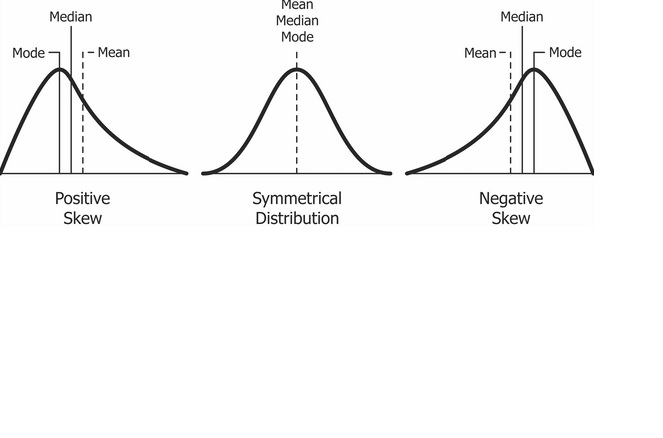
• Mod < Medyan < A. O olduğu durumda dağılımda sağa (pozitif) çarpıklık söz konusudur.
• Mod = Medyan = A. O olduğu durumda dağılım simetriktir.
• Mod > Medyan > A. O olduğu durumda dağılımda sola (negatif) çarpıklık söz konusudur.

Bu yazımızda uçtan uca bir çalışmada elimizde bulunan veri hakkında genel fikir sahibi olmak ve veriyi anlamak için yapılan en önemli basamaklardan biri olan ve veriyi tanımlayan, tanımlayıcı istatistik adı altında yer alan ölçütleri inceledik. Bu ölçütler, analiz sürecinin temelini oluşturmakla birlikte veri seti hakkında birçok önemli bilgiyi edinmemizi sağlar. Tanımlayıcı istatistik başlığı altında gözlemlerin birbirleri arasındaki uzaklıklarına ilişkin ölçütleri barındıran Dağılım Ölçülerine de Miuul Not Defteri’nden ulaşabilirsiniz. 

Kaynaklar

• Larsen, R. J., & Marx, M. L. (2005). An introduction to mathematical statistics. Prentice Hall.
• Hogg, R. V., & Craig, A. T. (1995). Introduction to mathematical statistics.(5th edition). Englewood Hills, New Jersey.
• Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.
• İkiz, F., Püskülcü, H., & Eren, Ş. (2000). İstatistiğe giriş. Barış Yayınları Fakülteler Kitabevi.
• Akdeniz, F. (2012). Olasılık ve İstatistik, 17. Baskı, Nobel Kitabevi, Adana.
• Veri Bilimi Okulu, Merkezi Eğilim Ölçüleri
• Veri Bilimcisi, Merkezi Eğilim Ölçüleri