Ortalama ve Medyan Arasında Ne Fark Var?
Ortalama ve Medyan’ın ne anlama geldiklerinden Merkezi Eğilim Ölçüleri yazımızda kadar bahsetmiş olsak da bu yazımızda konuyu biraz daha detaylandırarak önemi üzerinde duralım.
Her iki ölçüt de veri kümesinin merkezinde veya orta değerinin etrafında kümelenme eğilimini ifade eder. Veri setinin merkezi değerine “ortalama”, orta değerine ise “medyan” ile ulaşırız.
Ortalama
Ortalama; temelinde bir veri kümesindeki değerlerin toplamlarının veri kümesindeki değer sayısına bölünmesi ile elde edilir. İstatistikte kitle ortalaması ve örneklem ortalaması olarak iki ayrı şekilde ifade edilir.
Burada;
- μ : Kitleye ilişkin aritmetik ortalamayı,
- x : Örnekleme ilişkin aritmetik ortalamayı,
- N : Kitlenin toplam gözlem sayısını,
- n : Örneklemin toplam gözlem sayısını ve
- xi : i. gözlem değerini temsil etmektedir.
Kitle ortalaması, üzerinde çalışılacak tüm popülasyonda yer alan gözlem değerlerinden elde edilirken; örneklem ortalaması ilgilenilen popülasyon içinden kitleyi en iyi yansıtan bir parçasından elde edilir. Genellikle çalışmalarda hem zaman hem de maliyet sebebiyle tüm kitleye ulaşmak zahmetli olduğundan kitleyi en iyi temsil eden örneklemler üzerinden modeller geliştirilir.
Ortalamayı kitle ortalaması ve örneklem ortalaması olarak üzerinde çalışılacak parçaya göre iki ayrı şekilde inceliyor olsak da ortalamayı hesaplarken karşılaşılan bazı özel durumların var olduğuna Merkezi Eğilim Ölçüleri yazımızda da değinmiştik. Bu özel durumlar gözlemlerin frekans sıklığı ve derecesine göre değişkenlik göstermektedir. Gözlemlerin frekanslarının göz önünde bulundurularak yapılan hesaplamalarda Sınıflandırılmış Aritmetik Ortalama, gözlemlerin derecelerinin göz önünde bulundurularak yapılan hesaplandırmada ise Gruplandırılmış Aritmetik Ortalama kullanılmaktadır.
Medyan
Bir diğer ifadeyle Ortanca veya Orta Değer olarak bilinen Medyan ise; tüm veri setindeki değerlerin küçükten büyüğe doğru sıralandığında en ortada yer alan değeri ifade etmektedir. Buradaki ayrım ise veri setinde yer alan gözlem sayısından kaynaklanmaktadır. Gözlem sayısının çift veya tek değer oluşuna göre medyanın hesaplaması değişmektedir.
Burada;
- n: Gözlem sayısını,
- j: Gözlem değerinin kaçıncı gözlem olduğunu,
- xj: j. gözlem değerini temsil etmektedir.
Her ne kadar en popüler merkezi eğilim ölçüsü ortalama olsa da bazı durumlarda medyan kullanılmasının sebebi nedir? Hemen hemen aynı anlama gelen bu iki ölçütü birbirinden farklı kılan durumlar nelerdir?
Merkezi eğilim ölçülerinin temelinde; açıkça tanımlanabilen, kolay anlaşılan, basitçe hesaplanabilen ölçüt olma özelliği vardır. Tüm gözlemleri yansıtması ve aykırı değerlerden olabildiğince az etkilenmesi beklenir.
Bunu basit bir örnekle aşağıdaki gibi açıklayabiliriz.
- Bir sınıftaki 10 öğrencinin yaşları:
22, 18, 19, 51, 20, 21, 19, 19, 18, 25
- Öğrencilerin yaşlarının aritmetik ortalaması
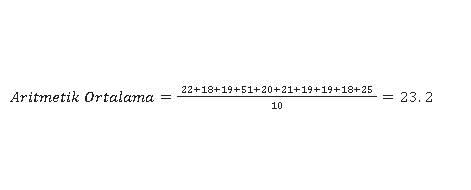
- Medyan değeri, küçükten büyüğe sıralandığında gözlem sayısı 10 olduğundan orta değer 5. ve 6. gözlemlerin ortalamasıdır:
18, 18, 19, 19, 19, 20, 21,22, 25, 51
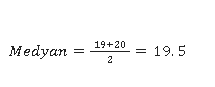
Bu örnek içim, iki ölçüte göre topluluğu en iyi yansıtan değer hangisidir?
Veri kümesindeki öğrenciler genel itibariyle 19, 20’li yaşlarında iken 51 yaşındaki bir kişinin veri kümesine dahil olması ile aritmetik ortalama oldukça değiştirecek ancak medyan özelinde radikal bir değişikliğe neden olmayacaktır. Bu durum medyan değerinin veri kümesini aritmetik ortalamadan daha iyi temsil ettiği sonucunu çıkarmaktadır.
Yukarıdaki örnekte veri kümesini en iyi tanımlayan ölçüt medyandır. Hangi ölçütün veri kümesini en iyi şekilde yansıttığını belirlemek oldukça önem arz etmektedir. Bu aşamada ölçütler arasındaki farkları bilme ihtiyacı ortaya çıkar. Anlatılanlara ek olarak ortalama ve medyan arasındaki temel farklar aşağıdaki tabloda yer almaktadır.
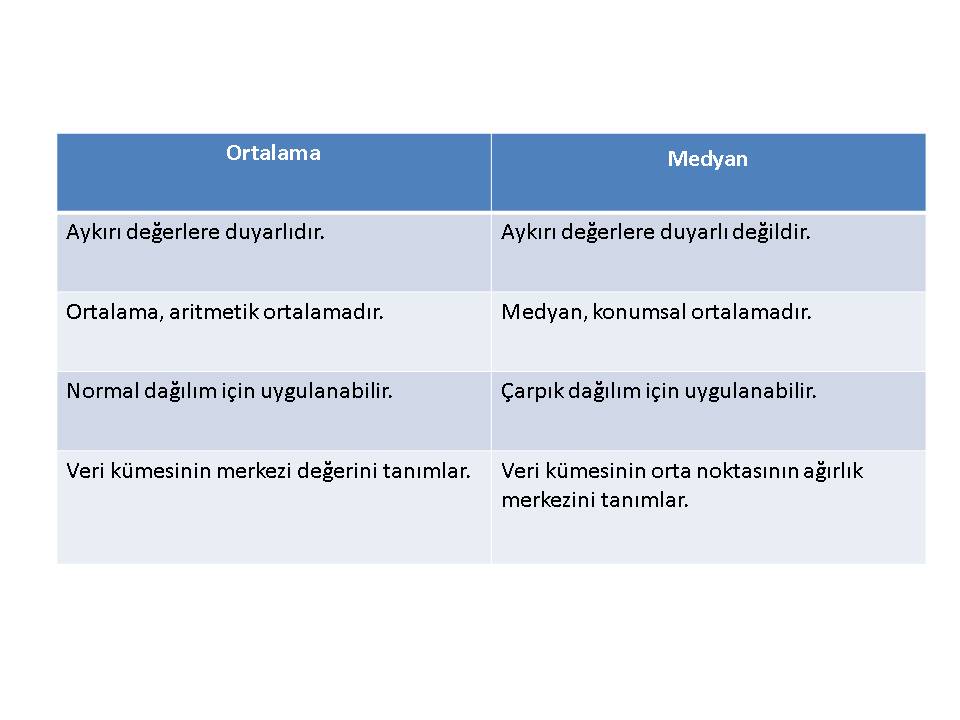
Yukarıdaki iki ölçüt arasındaki farkları gösteren tabloda veri setinin dağılımına, merkezi değerinin ne olduğuna, duyarlılığına göre kullanılacak metriğin veri setinin olabilecek en doğru şekilde yansıtılmasında oldukça önemlidir. Buradaki temel amaç, veri setini en doğru şekilde ifade etmektir. Veri setini ifade etmek için kullanılan başka metrikler de mevcuttur. Bu yazıda her ne kadar iki metriğin karşılaştırılması üzerine yoğunlaşmış olsa da diğer metriklerle ilgili detaylı bilgilerin yer aldığı Merkezi Eğilim Ölçüleri başlıklı yazıya Miuul Not Defteri’nden ulaşabilirsiniz.
Kaynaklar
- Larsen, R. J., & Marx, M. L. (2005). An introduction to mathematical statistics. Prentice Hall.
- Hogg, R. V., & Craig, A. T. (1995). Introduction to mathematical statistics.(5th edition). Englewood Hills, New Jersey.
- Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.
- İkiz, F., Püskülcü, H., & Eren, Ş. (2000). İstatistiğe giriş. Barış Yayınları Fakülteler Kitabevi.
- Akdeniz, F. (2012). Olasılık ve İstatistik, 17. Baskı, Nobel Kitabevi, Adana.
- Veri Bilimi Okulu, Merkezi Eğilim Ölçüleri
- Veri Bilimcisi, Merkezi Eğilim Ölçüleri
