Matrislere Giriş ve Python'da Matrisler

Bu yazıda matrislere ilişkin temel bilgileri aktarıyor ve konuyla ilgili bazı Python uygulamaları gerçekleştiriyorum.

Nehir Günce Daşcı • 07 Nis 2021

Matris kısaca sayıların satırlar ve sütunlar üzerinde düzenlenmiş halidir. Gözlem sayısının n, değişken sayısının p ile ifade edildiği matrisin boyutu nxp olarak belirtilir.

Python’da matrisler için yerleşik tür yoktur. Fakat iç içe liste yöntemiyle basit hesaplamalar yapılabilir ya da NumPy paketi ile matrislerle etkili bir biçimde çalışılabilir. Liste, aslında tek boyutlu bir veri yapısıdır. İki boyutlu listeler matris olarak bilinir.

Örnek 1: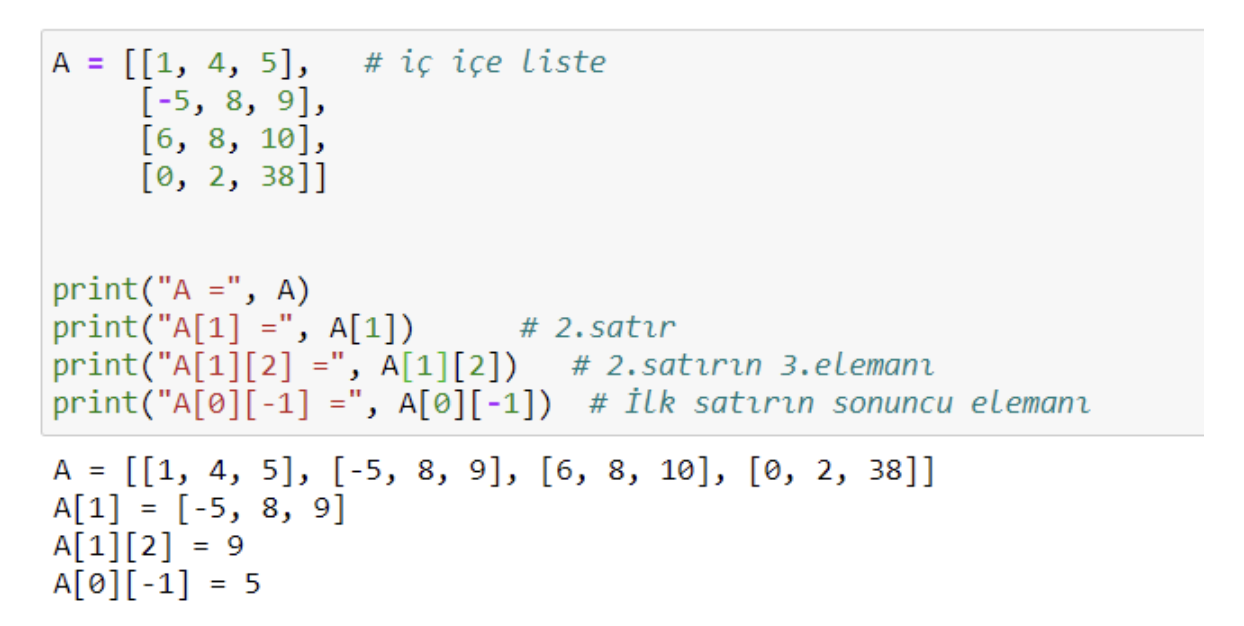

Örnek 2: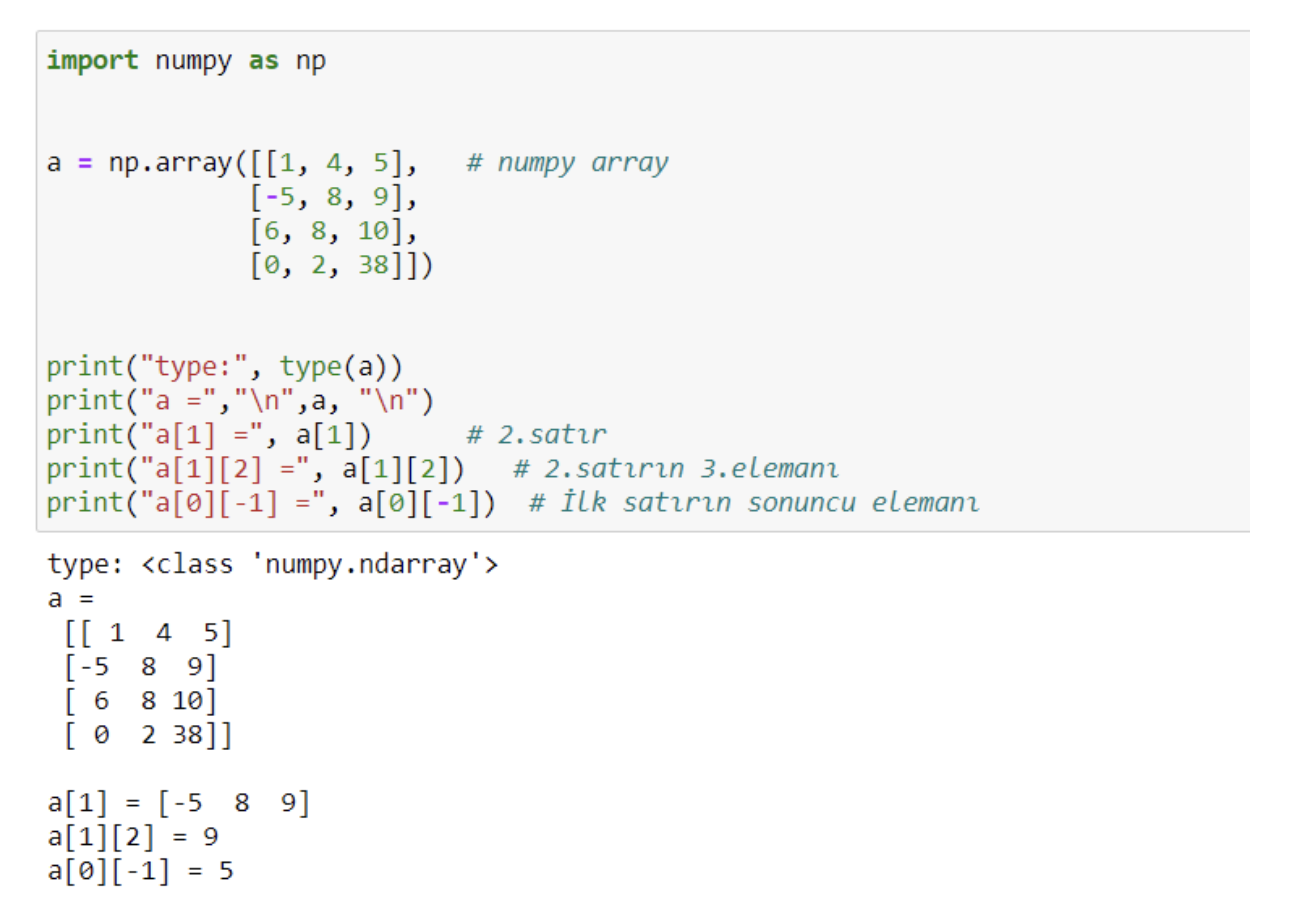

a matrisi

Matris Türleri

Farklı matris çeşitleri bulunmaktadır. Kare matriste satır sayısı (n) ile sütun sayısı (p) birbirine eşittir.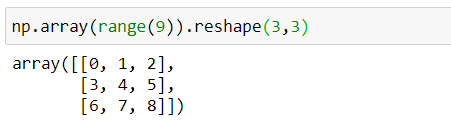

3x3 boyutlu kare matris

Sıfır matrisin ise tüm elemanları 0'dır.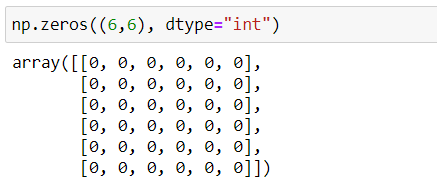

Not: Default çıktı float olarak dönüyor, integer'a çevirdim.

Sadece 1 satırı olan matrise satır matrisi, sadece 1 sütunu olan matrise sütun matrisi denir.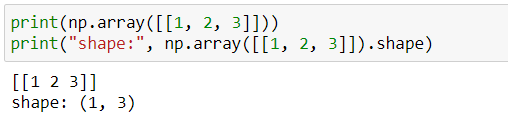

Satır matrisi: 1x3 boyutlu, satır sayısı 1

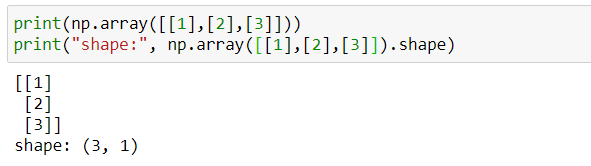
Sütun matrisi: 3x1 boyutlu, sütun sayısı 1

Köşegen elemanları dışındaki tüm elemanları 0 olan matris ise köşegen matris olarak bilinir. Sadece kare matrisler, köşegen matris olabilir.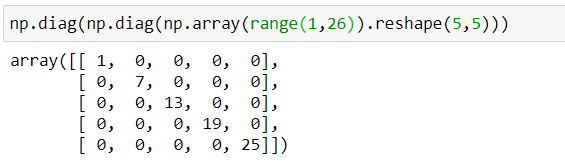

Matris kare iken (yani n=p iken), köşegen elemanların 1 kalan elemanların 0 olduğu matris ise birim matristir.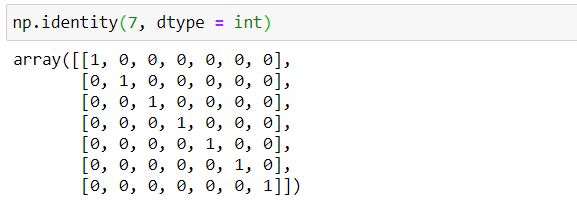

Esas köşegen üzerindeki elemanları aynı olup kalan elemanları 0 olan matris ise skaler matris olarak isimlendirilir. Birim matrisin bir skaler ile çarpılması sonucu elde edilir.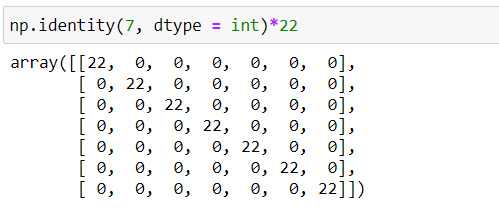

Bir matrisin (örneğin A matrisi) satırları ile sütunlarının yer değiştirmesi sonucu oluşan matris ise transpose (devrik) matristir. Aᵀ ile gösterilir.

Kolay yoldan devrik matris oluşturma: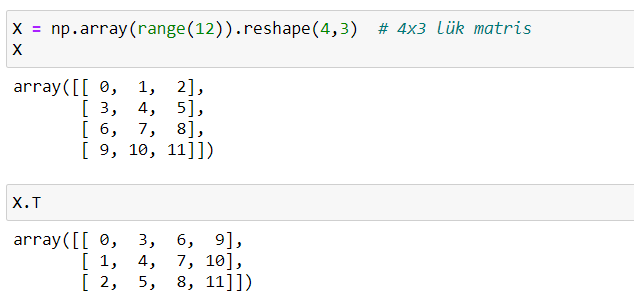

Döngü yardımıyla devrik matris oluşturma: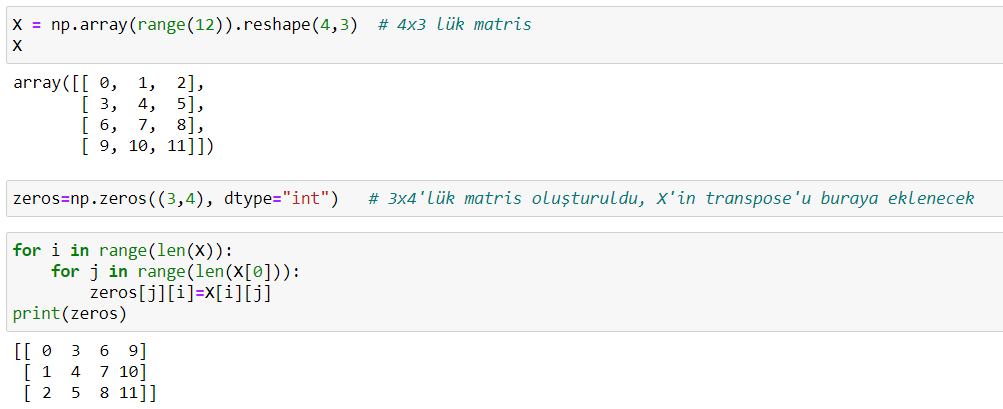

List comprehension ile devrik matris oluşturma: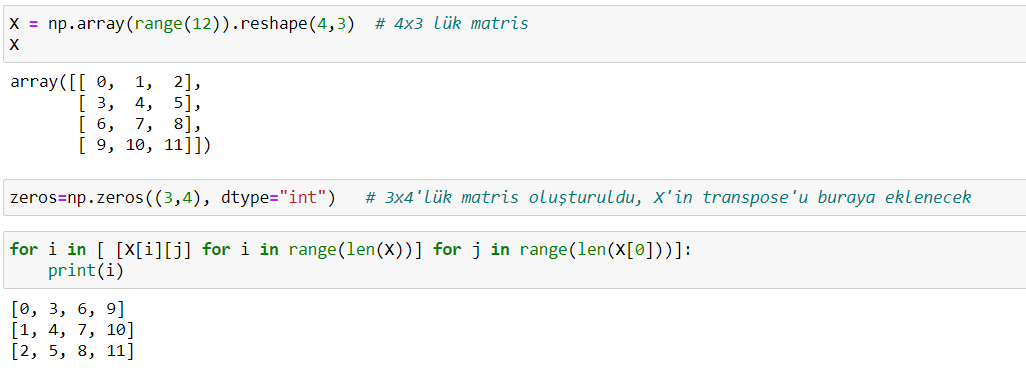

Matrislerde toplama ve çıkarma işlemleri

Matrislerde toplama çıkarma işlemleri için ilgili matrislerin boyutlarının aynı olması gerekir.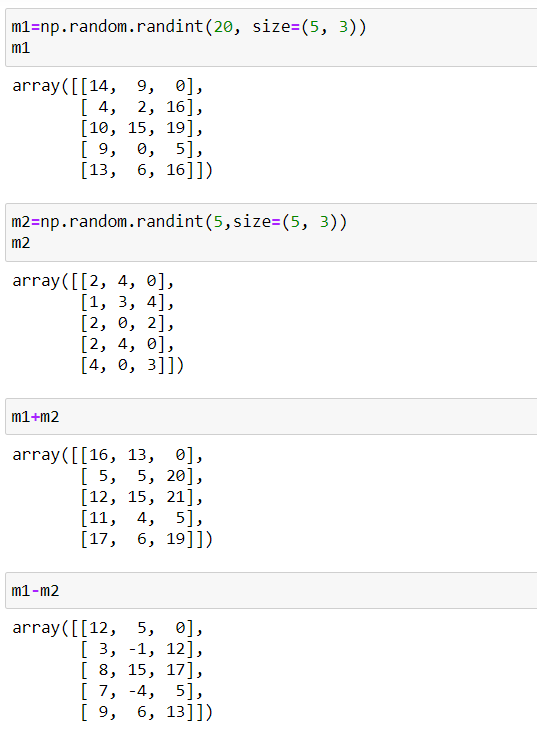

Matrislerde çarpma işlemi

Matrisin belirli bir sayı ile çarpımında matristeki her bir eleman sabit sayı ile çarpılır.

Matrisin matris ile çarpımı ise klasik çarpma işleminden farklıdır ve görece daha karmaşıktır. İlk matrisin sütun sayısının ikinci matrisin satır sayısına eşit olması gerekir. Ortaya çıkan yeni matrisin satır sayısı ilk matrisin satır sayısına; sütun sayısı ikinci matrisin sütun sayısına eşittir. Python’da bu işlem döngü ile yapılır.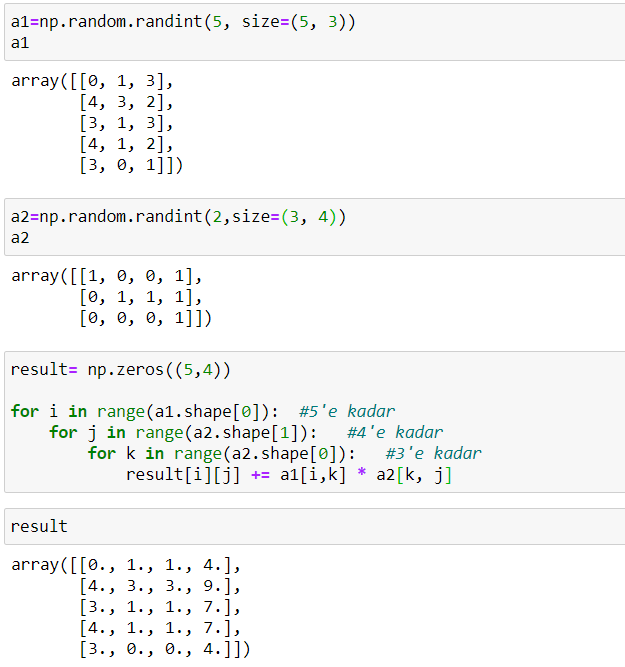

1. Adım: İlk matrisin ilk satırı ile ikinci matrisin ilk sütunu birebir eşlenerek çarpılır, bu çarpımlar toplanır, sonuç matrisinde result[0][0]’lık kısma yazılır.
2. Adım: İlk matrisin ilk satırı ile ikinci matrisin ikinci sütunu birebir eşlenerek çarpılır, bu çarpımlar toplanır, sonuç matrisinde result[0][1]’lık kısma yazılır.
3. Adım: İlk matrisin ilk satırı ile ikinci matrisin üçüncü sütunu birebir eşlenerek çarpılır, bu çarpımlar toplanır, sonuç matrisinde result[0][2]’lık kısma yazılır.
4. Adım: İlk matrisin ilk satırı ile ikinci matrisin dördüncü sütunu birebir eşlenerek çarpılır, bu çarpımlar toplanır, sonuç matrisinde result[0][3]’lık kısma yazılır.
5. Adım: İlk arrayin ilk satırı için işlemleri tamamlandı. Bu dört adım ilk arrayin her bir satırı için yapılır.

Matrislerin bazı özellikleri

A, B,C birer matris ve r, s birer sabit sayı ve I’lar birim matris iken;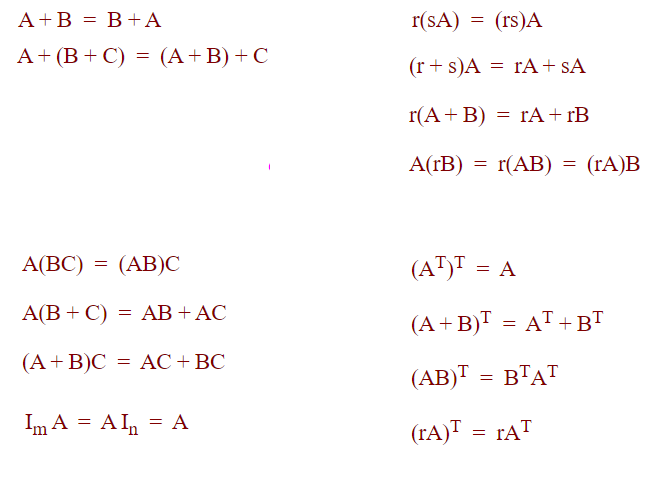

Matrisin tersi

A üzeri -1 ile gösterilir.

A matrisinin tersi ile sağdan ya da soldan çarpımı birim matrise eşittir. Bir matrisin tersinin alınabilmesi için kare matris olması şarttır.

2x2 boyutlu matrislerde hesaplanması kolaydır.

Determinant

Köşegen elemanların birbirleri ile çarpımından kalan elemanların birbirleri ile çarpımlarının çıkarılmasıdır. (1x3)-(1x1)

Tersi alınırken:

Köşegen elemanlar yer ve işaret değiştirir.
Her bir eleman determinanta bölünür.

Bu sebeple, matrisin determinantı 0'a eşitse, matrisin tersi yoktur. 2'den fazla boyutlar için pythonda direkt np.linalg.inv() komutunu kullanabilirsiniz.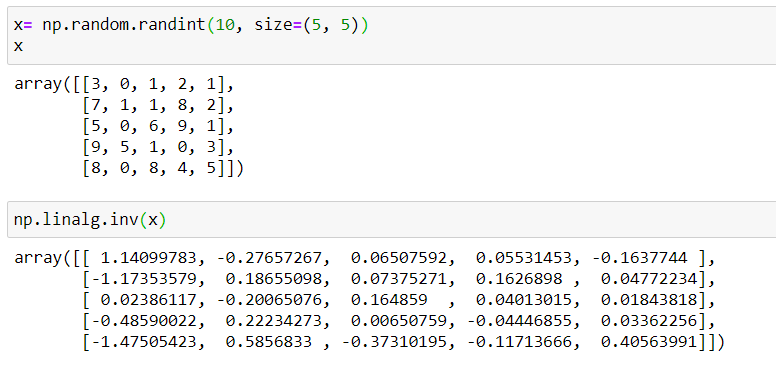

Python hakkında daha geniş kapsamlı bilgiye erişmek ve kariyerinizde Python bilginizle fark yaratmak isterseniz Miuul'un sunduğu Veri Bilimi için Python Programlama eğitimine göz atabilirsiniz.

Kaynaklar