Python ile Doğrusal Regresyon Uygulaması
Doğrusal regresyon, tahmin edilecek değeri ilişkisi olan diğer değişken veya değişkenlere dayalı olarak tahmin etmek için kullanılır. Tahmin edilecek değişken bağımlı değişken olarak adlandırılırken, tahmin değişkenini doğrudan etkileyen ve sonuca etkisi olan diğer değişkenlere de bağımsız değişken denir.
Doğrusal regresyon analizi bağımlı değişken ile bağımsız değişkenin/değişkenlerin arasındaki ilişkiyi çıkarmak için kullanılır. Bağımsız değişkenin bağımlı değişkeni ne şekilde etkilediğini bulmak için yapılan bir analizdir. Amaç bağımsız değişkenlerden bağımlı değişkeni en iyi temsil edecek matematiksel ifadeyi bulmaktır.
Doğrusal regresyon nasıl çalışır?
Doğrusal regresyon, sayısal girdileri sayısal çıktılarla eşleştirmemize ve veri noktalarına bir çizgi uydurmamıza izin veren bir makine öğrenimi algoritmasıdır. Basit doğrusal regresyon analizinde yer alan iki değişken, x ve y olarak adlandırılır. Bağımlı değişken y'nin, bağımsız değişken x ile nasıl ilişkili olduğunu açıklayan denklem, regresyon modeli olarak bilinir.
Basit doğrusal regresyon modeli şu şekilde temsil edilebilir:
y=b0+b1x
Burada, b0 ve b1 model parametreleri olarak adlandırılmaktadır.
- b0, sabit terimi yani doğrusal denklemin y ekseni ile kesişim noktasını temsil eder.
- b1, doğrunun eğimini yani bağımsız değişkenin bağımlı değişkene olan ağırlığını ifade eder.
Basit lineer regresyon denklemi, düz bir çizgi olarak grafiğe geçirilir.
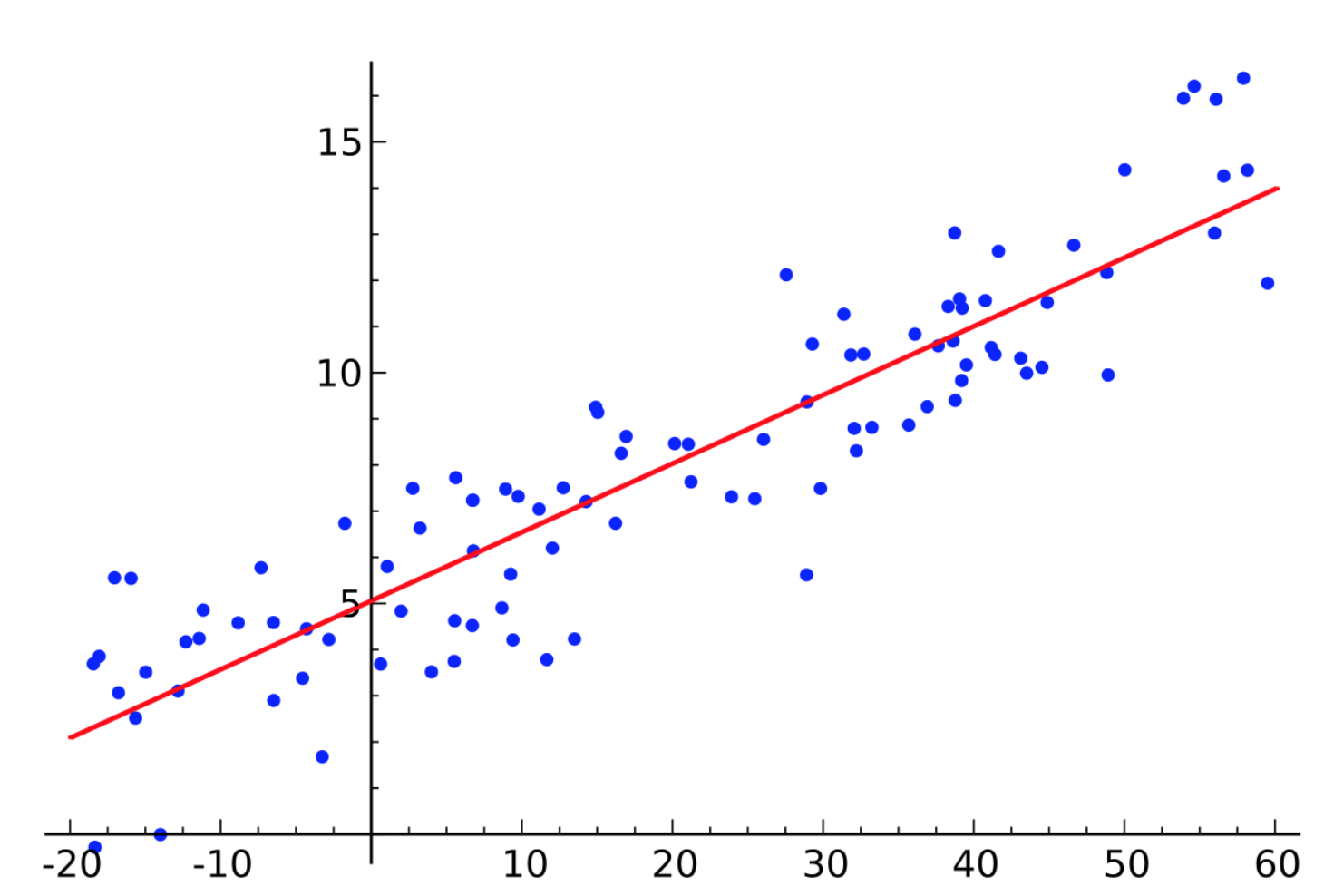
Doğrusal regresyon algoritmasının amacı, en uygun doğruyu bulmak için b0 ve b1 için en iyi değerleri elde etmektir. En uygun çizgi, tahmin edilen değerler ile gerçek değerler arasındaki farkın minimum olduğu yani en az hatanın elde edildiği çizgidir. Modelden elde edilen grafik, bağımsız değişkenlerin bağımlı değişkeni en iyi şekilde temsil ettiği parametreler ile oluşturulan denklemden elde edilmektedir.
Başarı değerlendirmesi nasıl yapılır?
Doğrusal regresyonda genellikle cost fonksiyonu olarak, tahmin edilen değer (y) ile gerçek değer (y) arasındaki farkın karesi ile hesaplanan Ortalama Kareler Hatası (Mean Squared Error, MSE) kullanılmaktadır.
Veri üzerine doğru çizmekteki amacımız model kurmaktır. X değerlerine karşılık Y değeri ne oluyor sorusunun cevabını veriye fit edilen doğruyu kullanarak yanıtlıyoruz. Peki bu doğru geçmiş veriyi iyi temsil edebilmiş mi? İyi bir model kurabilmiş miyiz? Bu soruların cevabını MSE değerini hesaplayarak alabiliriz.
MSE değeri hesaplanırken ortalama alınmasının sebebi, geneldeki ortalama hata değerini ölçmek istediğimiz içindir. Gerçek değerler ile tahmin edilen değerlerin arasındaki farkın karesinin alınmasının sebebi ise negatif değerden kurtulmak içindir.
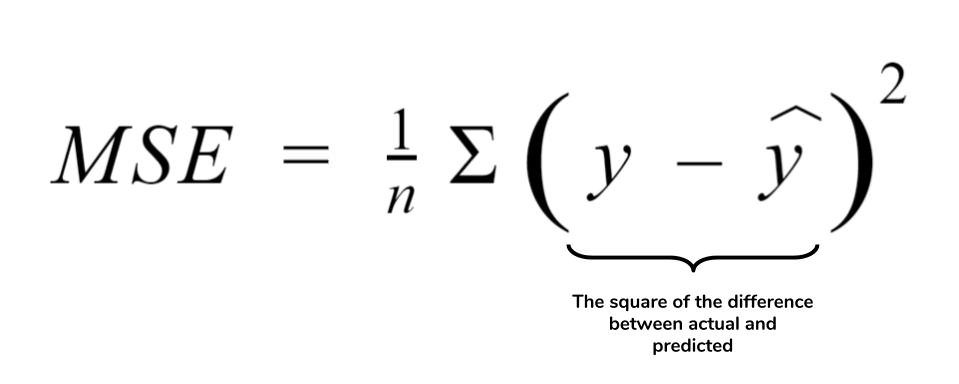
b0 ve b1 değerleri, MSE değeri minimum düzeyde olacak şekilde güncellenir. Bu parametreler, cost fonksiyonu için değer minimum olacak şekilde gradyan iniş (gradient descent) yöntemi kullanılarak belirlenebilmektedir.
Başarı değerlendirmesi için MSE mi MAE mi kullanmalıyız?
MAE(mean absolute error) yani ortalama mutlak hata hesaplanırken gerçek değerden tahmin edilen değer çıkartılıp sonucun mutlak değeri alınır, böylece negatif değerden kurtulmuş oluruz.
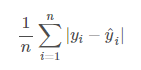
Peki modelin başarısını değerlendirirken MSE mi MAE mi kullanacağız? Aslında bunun net bir yanıtı yoktur. MSE hesaplamasında, bir nokta tahminimizin çok uzağında kalmışsa onu ekstradan karesini alarak fazladan cezalandırıyor. MAE hesaplamasında ise kare alınmıyor. MAE daha iyi bir tercih gibi görünse dahi her zaman bu yorumu yapamayız.
Performans değerlendirmesi yaparken büyük hatalar bizim için kritik ise o zaman bizim için doğru tercih o büyük hataları ekstradan cezalandıran MSE’dir. Ancak bizim için büyük hatalar önemli değilse, arada bir denk geliyorsa veya bu değerler outlier ise bu değerlerin abartılmasını isteyip MAE hesaplamasını tercih edebiliriz.
Temel yaklaşımı öğrendikten sonra kendi problemimiz için en uygun olanı tercih etmeliyiz.
Tek değişkenli lineer regresyon örnek uygulama
Kaggle’dan alınan, 205 satır ve 26 kolondan oluşan ve araç özelliği ile fiyat ilişkisini içeren bir veri seti olan araba verisi ile örnek bir basit lineer regresyon uygulaması ele alalım.
Araç fiyat alımlarında aracın motor boyutu arttıkça araç fiyatının da orantılı bir şekilde arttığı bilinen bir gerçektir. Aşağıda iki değişken arasındaki korelasyon da pozitif yönlü olmakla birlikte etkileri oldukça yüksek olduğu görülmektedir.
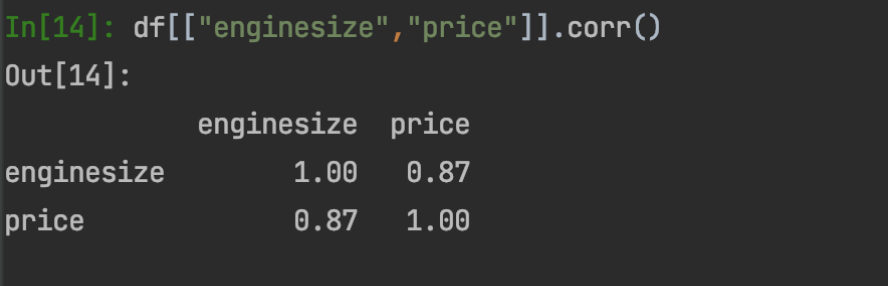
Problem tanımımız araç motor boyutundan araç fiyat eğrisini çıkaracak denklemi bulmaktır. Kullanacak olduğumuz kütüphaneleri import edip veriyi okutarak başlayalım.
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
df = pd.read_csv("miuul/CarPrice_Assignment.csv")
Lineer regresyonun verilen x değerlerini en iyi temsil edecek değerleri bularak y değerine ulaşabileceğimiz denkleme odaklanarak çalıştığını öğrenmiştik. Bu problemde de x, bağımsız değişkenimizi araç motor gücü olarak belirlerken, y bağımlı değişkenimizi yani tahmin edecek olduğumuz değişkeni de araç fiyatı olarak belirleyip lineer regresyon modelimizi kuruyoruz.
X = df[["enginesize"]]
y = df[["price"]]
reg_model = LinearRegression().fit(X, y)
Lineer regresyon denkleminin oluşturulmasının ardından denklemi ifade edecek sabit ve x katsayısı hazırlanmış olur.
# sabit (b - bias)
reg_model.intercept_[0]
# -8005.445531145215
# motor gücünün'nin katsayısı (x1)
reg_model.coef_[0][0]
# 167.69841639317224
x’in katsayısının 0’dan büyük olması eğilimin pozitif yönde olduğunu yani bir değişkenin artışının diğer değişkeni de arttırdığını ifade etmektedir. Çalışmanın başında yapılan korelasyon analizinde de bu bulgumuzla paralel şekilde örneğimizde yönün pozitif olduğunu gözlemlemiştik.
Şimdi bir de model denklemini çizip modelin gerçek y değerlerini nasıl temsil ettiğine bakalım.
g = sns.regplot(x=X, y=y, scatter_kws={'color': 'b', 's': 9},
ci=False, color="r")
g.set_title(f"Model Denklemi: Fiyat = {round(reg_model.intercept_[0], 2)} + Araç Motor Gücü * {round(reg_model.coef_[0][0], 2)}")
g.set_ylabel("Araç Fiyatı")
g.set_xlabel("Araç Motor Gücü")
plt.xlim(40, 300)
plt.ylim(bottom=0)
plt.show()
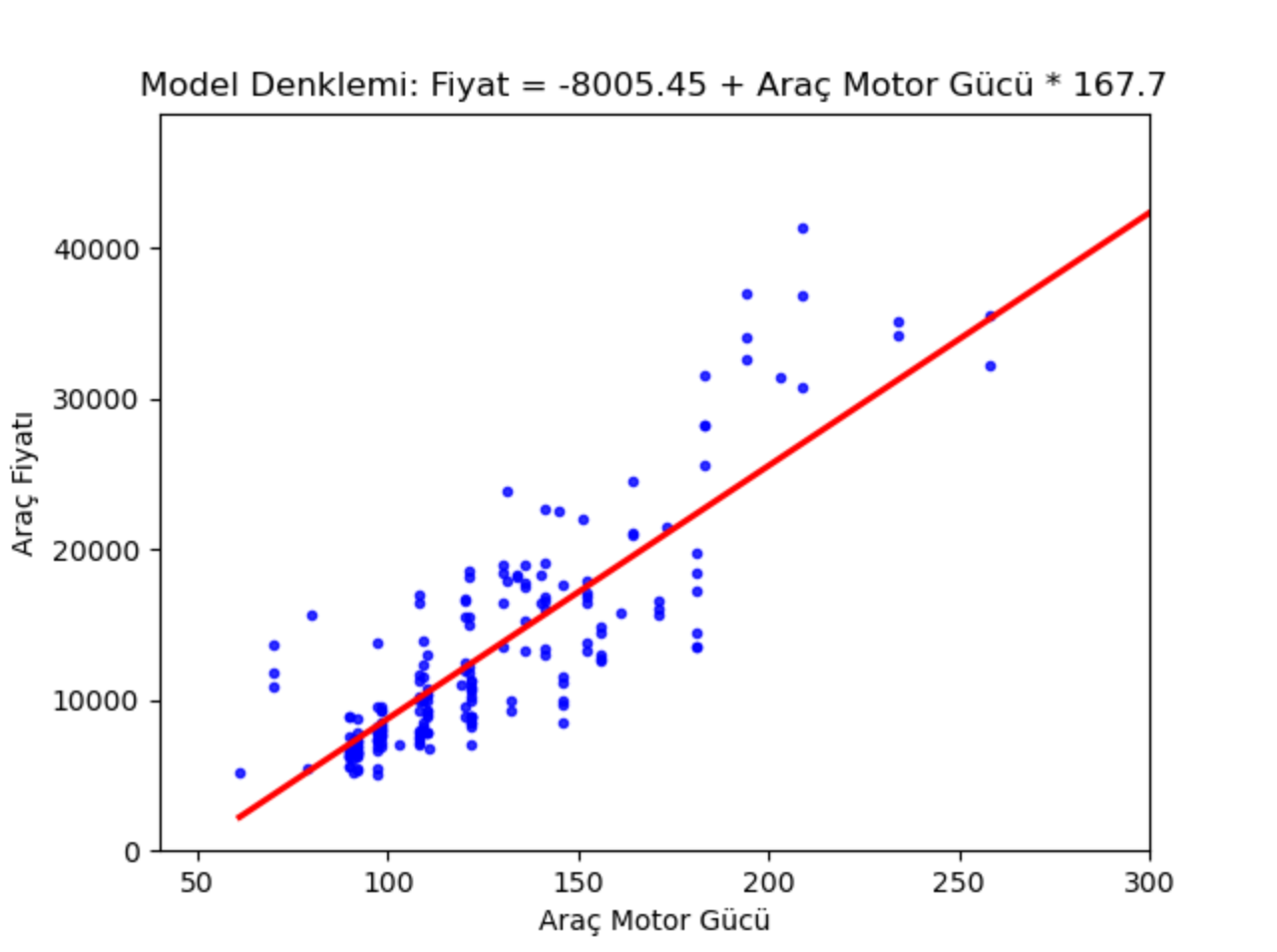
Elde edilen denklemde de görüldüğü gibi motor gücünün artışı araç fiyatının da artmasına neden olmaktadır. MAE ile model başarısı incelenirse;
# MAE
y_pred = reg_model.predict(X)
mean_absolute_error(y, y_pred)
# 2815.0223538364103
Elde edilen MAE neticesinde, doğrusal regresyon analizi ile kurulan model ile yapılan tahminlerde ortalama 2815 birimlik bir sapma mevcuttur.
130 motor gücüne sahip bir araç için fiyat tahmini yapılmak istenirse:
reg_model.intercept_[0] + reg_model.coef_[0][0]*130

13795 birimlik bir fiyat tahmini elde edilecektir.
Çok Değişkenli Lineer Regresyon Örnek Uygulama
Aynı veri seti ile birden fazla kolonla (bağımsız değişkenle) bir lineer regresyon denklemi oluşturalım. Bağımlı y değişkenimiz yine araç fiyatı olsun. Ancak bağımsız değişkenler, x, içerisinde hem kategorik hem de nümerik değişkenlerin mevcut olsun.
Gerekli kütüphaneleri import edip veriyi okuyarak başlayalım.
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
df = pd.read_csv("miuul/CarPrice_Assignment.csv")
Veri içerisinde hem nümerik hem de kategorik değişkenler olduğu için kategorik değişkenlere one-hot dönüşümü, nümerik değişkenlere ise standartlaştırma uygulayabilmek için hepsini liste içerisinde list comprehension yapısını kullanarak tutabiliriz.
# kategorik değişkenlere one-hot dönüşümü, nümerikleri de standarlaştırma işlemine tabi tutuyoruz.
cat_cols = [col for col in df.columns if df[col].dtypes == "O"]
num_cols = [col for col in df.columns if df[col].dtypes != "O"]
num_cols = [col for col in num_cols if col not in ["price","car_ID"]]
df.drop(["car_ID","CarName"], axis=1, inplace=True)
Özellik mühendisliği ve model öncesi yapılması gereken veri ön işleme adımlarının detaylı bir şekilde anlatıldığı Özellik Mühendisliği kursuna linkten göz atabilirsiniz.
def one_hot_encoder(dataframe, categorical_cols, drop_first=False):
dataframe = pd.get_dummies(dataframe, columns=categorical_cols, drop_first=drop_first)
return dataframe
df = one_hot_encoder(df, cat_cols, drop_first=True)
X_scaled = StandardScaler().fit_transform(df[num_cols])
df[num_cols] = pd.DataFrame(X_scaled, columns=df[num_cols].columns)
Artık verimiz hazır olduğuna göre lineer regresyon modelimizi kurabiliriz.
y = df["price"]
X = df.drop(["price"], axis=1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=1)
reg_model = LinearRegression().fit(X_train, y_train)
Elimizde artık doğrusal regresyon ile elde edilmiş bir denklem bulunmakta. Bu denklemin bir sabit değişkeni ve her değişken için de bir katsayısı mevcuttur. Görülebildiği üzere 47 kolonun her biri için bir katsayısı üretilmiş halde, yani her kolonu en iyi şekilde temsil edecek bir katsayı mevcuttur.
# reg_model.intercept_
# 20041.41
reg_model.coef_
# array([ 5.39588633e+02, -1.78713787e+03, 2.39781569e+03, 3.28027797e+02,
# 2.29881074e+03, 4.65908934e+03, -8.52739090e+02, -1.24347703e+03,
# -2.19864128e+03, 5.65509807e+01, 5.09436456e+02, -9.63946800e+02,
# 8.78647266e+02, -4.25498092e+03, 1.43384818e+03, -1.88342792e+02,
# -4.45728957e+03, -3.58118058e+03, -2.57206173e+03, -3.56256776e+03,
# 5.19361989e+02, 2.61287928e+03, 1.28593641e+04, -5.96185944e+03,
# -4.27102079e+03, 2.19707941e+03, 8.23388257e+02, -4.72886444e+03,
# 6.47703996e+02, -6.89856736e+03, -6.30369570e+03, -5.32167600e+03,
# 0.00000000e+00, -9.75298980e+03, 6.47703996e+02, -3.87716648e+01,
# 6.47703996e+02, 4.25498092e+03, -9.09494702e-13, 3.85729991e+02,
# -1.33378770e+03, -1.24041520e+03, 1.23764730e+03, 3.07681502e+03,
# 3.24314969e+03, 2.89592359e+03, 1.52171166e+03])
X.shape[1]
# 47
len(reg_model.coef_)
# 47
Peki model başarımız ne durumda?
y_pred = reg_model.predict(X_test)
mean_absolute_error(y_test, y_pred)
# 1956.35
Gözüktüğü üzere çok değişkenli doğrusal regresyon ile yalnızca bir değişkene bağlı olarak kurduğumuz basit lineer regresyona oranla daha iyi bir MAE sonucuna erişebilmekteyiz.
Her bir denemede hesaplanan cost fonksiyonu ile parametrelerini güncelleyen yapı; eğitimde öğrenci başarısı hesaplama, basit yapıda performans/fiyat tahminleri gibi bir denklem ile çözülebilecek birçok yapıda kullanılabilmektedir.
Doğrusal regresyon ve makine öğrenmesi konularında daha fazla bilgiye sahip olmak için Miuul’un sunmuş olduğu tekil Makine Öğrenmesi kursunu inceleyebilir veya veri bilimi kariyerinizde kendinizi bir adım daha ileriye taşımak isterseniz Data Scientist Path’e göz atabilirsiniz.
Kaynaklar
- Miuul, Özellik Mühendisliği
- Miuul, Makine Öğrenmesi
- scikit-learn, Linear Regression
- SEM, Lineer Regresyon Modellemesi ile Pazarlama Kampanyaları Bütçe Estimasyonu
- Çaylı U., Medium, Linear Regression (Doğrusal Regrasyon) Nedir?
- Kaggle, Car Price Prediction Multiple Linear Regression
